Nach den drei Folgen über allerlei Exoten unter den Polyedern ist es vielleicht Zeit für ein bisschen Systematik. Es soll also diesmal weniger darum gehen, Schmetterlinge zu sammeln, als sie einzuordnen und dadurch einen besseren Überblick über den großen, bunten Zoo zu gewinnen.

Ich hatte schon mehrfach darauf angespielt, dass es die beiden großen Familien der Vierzähligen und der Fünfzähligen gibt. Dazu kommen eigentlich noch die Dreizähligen, zu denen das Tetraeder gehört; aber die werden meistens als die armen Verwandten der Vierzähligen bei diesen mit untergebracht. Wie sind diese Familien genau zu charakterisieren? Bisher habe ich nur von den vier- und den fünfzähligen Drehachsen gesprochen, welche die Mitglieder der jeweiligen Familie auszeichnen: Nach einer Viertel- (Fünftel-) Drehung um eine dieser Achsen sieht das Mitglied der entsprechenden Familie wieder genauso aus wie zuvor.

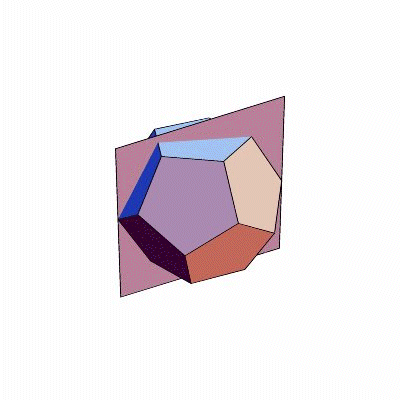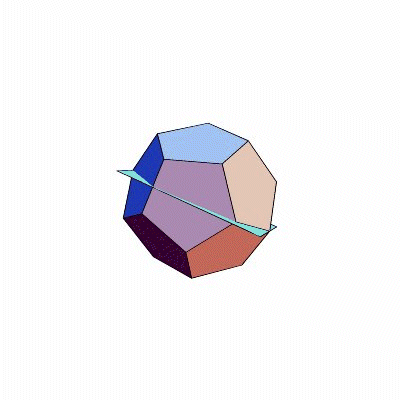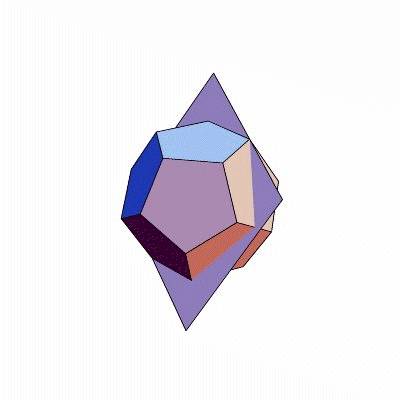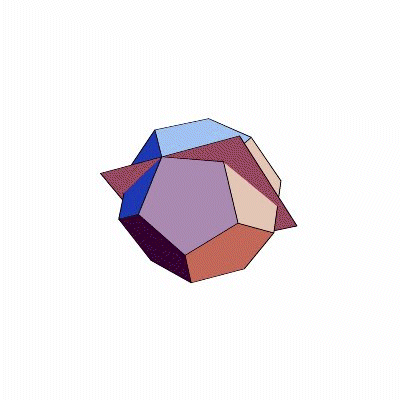
Allerdings: Eine dieser Drehachsen, und sei es eine mit der richtigen Zähligkeit, macht aus dem Polyeder noch kein Mitglied der Familie. (Das fünfseitige Prisma darf sich nicht zu den Fünfzähligen zählen.) Es muss schon das komplette Sortiment der Drehachsen sein. Und wie kommt das zu Stande? Das erzähle ich Ihnen jetzt. Nehmen wir den Urvater und die Urmutter aus der Familie der Fünfzähligen: das Dodekaeder und das Ikosaeder. (Welches von beiden Vater und welches Mutter ist, dürfen Sie sich aussuchen.) Setzen wir sie so ineinander, dass ihre Dualität am schönsten sichtbar ist, das heißt so, dass stets eine Kante vom einen Körper und eine vom anderen Körper einander halbieren und aufeinander senkrecht stehen. In dieser Position ist nämlich jede Symmetrie des einen Körpers auch eine des anderen.

Damit es hinterher einfacher ist, fangen wir nicht gleich mit den Drehungen an, sondern mit den Spiegelungen. Dodekaeder und Ikosaeder haben nämlich Symmetrieebenen: Spiegelt man den Körper an einer dieser Ebenen, sieht er genauso aus wie zuvor. Wie liegen diese Ebenen? Eine Ebene ist definiert durch drei Punkte. Ein Punkt jeder Symmetrieebene ist auf jeden Fall der gemeinsame Mittelpunkt der beiden Körper. Zwei brauchen wir noch; um die zu bestimmen, gibt es mehrere Möglichkeiten. Zum Beispiel kann man die zwei Endpunkte einer Kante nehmen; denn eine Ebene, die durch den Körpermittelpunkt und eine Kante geht, ist eine Symmetrieebene. Schauen Sie nach (Bilder)! Durch weiteres scharfes Hinschauen erkennt man: Unsere Ebenen gehen stets nicht nur durch eine Kante, sondern auch durch die genau gegenüberliegende, parallele Kante. Ansonsten gibt es keine Kante, die in derselben Ebene läge. Da sowohl Dodekaeder als auch Ikosaeder genau dreißig Kanten haben, kommt man so auf fünfzehn verschiedene Symmetrieebenen.

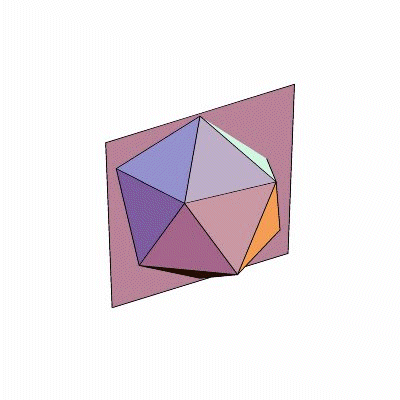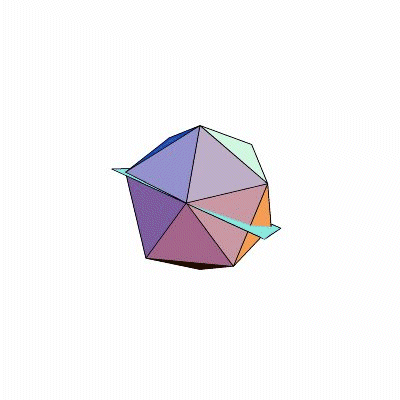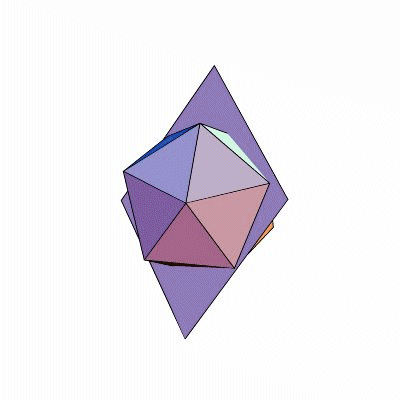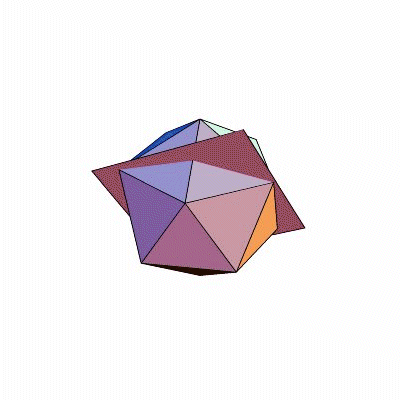
Und das sind auch schon alle! Sicher: Man kann jedes Fünfeck eines Dodekaeders halbieren, indem man eine Ecke mit dem Mittelpunkt der gegenüberliegenden Kante verbindet. Diese beiden Punkte mitsamt dem Körpermittelpunkt geben auch eine Symmetrieebene; aber die hatten wir alle schon. Jedes Fünfeck des Dodekaeders wird von fünf Symmetrieebenen durchschnitten und dadurch in zehn kleine Dreiecke zerteilt. Jedes dieser Dreiecke besteht aus Flächenmittelpunkt, Eckpunkt und benachbartem Kantenmittelpunkt.

Mit dem Ikosaeder verhält es sich im Prinzip genauso. Wenn die beiden Körper einander in dualer Position durchdringen, wie oben angegeben, sind ihre Symmetrieebenen sogar dieselben. Die Eigenschaft, bezüglich dieser fünfzehn Ebenen symmetrisch zu sein, vererbt sich mit allem, was dazugehört, von Urvater und Urmutter auf alle Mitglieder der Fünfzähligen-Familie – mit gewissen Einschränkungen, von denen später die Rede sein wird.

Derselbe Sachverhalt andersherum ausgedrückt lautet: Spiegelung an einer der fünfzehn Ebenen ist eine Symmetrieoperation des Ikosaeders (bzw. Dodekaeders), das heißt sie lässt den entsprechenden Körper unverändert. Statt "Symmetrieoperation" sagt man häufig verkürzt "Symmetrie", was etwas gewöhnungsbedürftig ist: Eine Symmetrie bedeutet bei den Mathematikern nicht nur eine Eigenschaft (zum Beispiel dem eigenen Spiegelbild gleich zu sein), sondern auch eine Aktion (zum Beispiel das Spiegeln).

An mehreren dieser Ebenen hintereinander zu spiegeln ist ebenfalls eine Symmetrie(operation); und damit sind wir in einem besonders beliebten Gebiet der Mathematik angelangt: der Gruppentheorie. Keine Bange – wir wollen uns nicht länger dort aufhalten als unbedingt nötig und dann ganz schnell zurück zur räumlichen Geometrie; aber ein kurzer Überblick ist hilfreich.

Gruppentheorie handelt von Aktionen, die widerruflich sind. Spiegelungen sind ohne Zweifel widerruflich, denn der Widerruf einer Spiegelung ist die Spiegelung selbst: Zweimal dieselbe Spiegelung ausgeführt, und alles ist wieder beim Alten (einerlei, ob der gespiegelte Gegenstand symmetrisch war oder nicht). Jede Kongruenzabbildung (Verschiebung, Drehung, Spiegelung) ist widerruflich.

Die Gruppentheorie behandelt nun diese möglicherweise komplizierten Aktionen als elementare Objekte. Sie versucht sich so wenig wie möglich mit ihren individuellen Eigenschaften zu befassen, sondern vielmehr mit ihren Beziehungen untereinander, genauso wie sich die klassische Arithmetik eigentlich nicht für die persönlichen Eigenheiten irgendwelcher Zahlen interessiert, sondern für deren Beziehungen, sprich das Rechnen. Am schönsten wäre es, wenn man die Beziehungen unter unseren Abbildungen so einfach formulieren könnte wie Rechenregeln. Das gelingt zwar nicht ganz, aber man kommt mit dieser Idee überraschend weit.

Der Multiplikation unter Zahlen entspricht die Hintereinanderausführung zweier solcher Aktionen: Spiegelung um eine Ebene, dann Spiegelung um eine andere Ebene. Diese Verknüpfung zweier Abbildungen wird wie eine Multiplikation angesehen und auch so geschrieben. Jetzt nehmen wir ein gewisses Grundsortiment an Symmetrien, nämlich die Spiegelungen an unseren fünfzehn Ebenen, und schauen nach, was herauskommt, wenn man beliebige Produkte dieser Symmetrien nimmt.

Geben wir jeder der fünfzehn Spiegelungen einen Namen, a, b, c, …, o, dann würde das heißen, wir betrachten alle "Wörter", die aus irgendeiner (endlichen) Folge dieser Buchstaben bestehen: lhjmnfa wäre so ein Wort, ngbhcb ein anderes und ccfagj ein drittes, aber das wäre dasselbe wie fagj, denn jede Spiegelung ist gleich ihrem Widerruf, weswegen wir Faktoren der Form xx sofort weglassen können. Das Wort aa ist dementsprechend gleich dem leeren Wort, das keine Buchstaben enthält und das wir deswegen mit 1 bezeichnen, damit man es überhaupt sehen kann. Warum 1? Weil es das neutrale Element der "Multiplikation" ist: 1x = x für jedes Wort x.

Jedes dieser Wörter steht für eine Kongruenzabbildung, nämlich diejenige, die aus all diesen Spiegelungen – in der angesagten Reihenfolge – besteht. ab bedeutet "zuerst Spiegelung b anwenden, dann auf das Ergebnis Spiegelung a". (Die Reihenfolge der Abbildungen ist standardmäßig von rechts nach links.) Das leere Wort steht für Nichtstun, und das ist offensichtlich auch eine Kongruenzabbildung.

Die Menge all dieser Wörter ist ein Beispiel für das, was die Mathematiker eine Gruppe nennen. Das Produkt zweier Wörter ist wieder ein Wort (das entsteht, indem man einfach die Faktoren ohne Lücke hintereinander schreibt), es gibt ein neutrales Element, nämlich das leere Wort, und jedes Wort hat sein "Widerwort" (offiziell heißt es "inverses Element"), das ist einfach dasselbe Wort mit der umgekehrten Buchstabenfolge. Denn wenn man Wort und Widerwort hintereinander schreibt (miteinander multipliziert), dann treffen in der Mitte nacheinander lauter Paare gleicher Buchstaben aufeinander, vernichten sich gegenseitig, und übrig bleibt das leere Wort. Diese drei Bedingungen (plus ein paar Formalitäten) sind das, was eine Gruppe ausmacht. Ob die Elemente der Gruppe nun Zahlen oder Symmetrieoperationen sind, oder bedeutungslose Buchstaben, für die man sich hinterher erst eine Bedeutung ausdenkt: Darauf kommt es vom abstrakten Standpunkt der Gruppentheorie nicht an.

In unserem konkreten Fall wollen wir natürlich schon wissen, was ein Wort wie ab bedeutet, was also passiert, wenn man zuerst die Spiegelung b und dann die Spiegelung a anwendet. Die Antwort ist: Zwei Spiegelungen um verschiedene Ebenen sind dasselbe wie eine Drehung. Dabei ist die Drehachse die Schnittgerade der beiden Ebenen, und der Drehwinkel ist gleich zweimal dem Winkel zwischen den Ebenen.

Nehmen wir zum Beispiel zwei Ebenen, die sich im Mittelpunkt eines Dodekaeder-Fünfecks schneiden (und natürlich in der ganzen Gerade, die durch diesen Mittelpunkt und den Kugelmittelpunkt geht). Eine soll durch eine Ecke des Fünfecks gehen und die andere durch den Mittelpunkt der angrenzenden Kante. Der Winkel zwischen diesen beiden Ebenen ist 36 Grad (ein Zehntel vom Vollwinkel); also sind die beiden Spiegelungen zusammen eine Drehung um 72 Grad (ein Fünftel vom Vollwinkel) um die Achse, die durch den Mittelpunkt des Fünfecks geht, und zwar linksherum oder rechtsherum je nachdem, in welcher Reihenfolge man die Spiegelungen anwendet. (ab ist also nicht dasselbe wie ba; die Gruppe ist nicht kommutativ!)

Da haben wir unsere fünfzählige Drehsymmetrie, und zwar um den Mittelpunkt jedes Dodekaederfünfecks. Die dreizählige Symmetrie um jeden Eckpunkt des Dodekaeders (oder, was dasselbe ist, Flächenmittelpunkt des Ikosaeders) und die zweizählige Drehsymmetrie um jeden Kantenmittelpunkt gewinnen wir auf dieselbe Weise. Es genügt nachzusehen, wie viele Spiegelungsebenen eine Achse gemeinsam haben, oder auch, wie viele unserer Großkreise durch ein und denselben Punkt auf der Kugeloberfläche gehen.

Für den abstrakten Standpunkt bedeutet das: Es müsste zwar theoretisch unendlich viele verschiedene Wörter geben – schließlich ist die Wortlänge nicht begrenzt; aber es gibt so viele Beziehungen zwischen den Wörtern, dass von den unendlich vielen Wörtern nur endlich viele übrig bleiben, die wirklich verschieden sind. Wenn zum Beispiel a und b unsere Spiegelungen von oben sind, dann ist ababababab = 1, denn fünfmal um 72 Grad um dieselbe Achse drehen ist dasselbe wie Nichtstun.

Wie viele verschiedene Abbildungen sind es denn nun, die man aus den fünfzehn Spiegelungen machen kann? Da muss man doch wieder sorgfältig nachzählen. Das Ergebnis ist: 120 Stück. "Die Symmetriegruppe des Ikosaeders hat 120 Elemente", ist die offizielle Formulierung.

Ein abstrakter Gruppentheoretiker kann mit der schieren Zahl 120 schon eine ganze Menge anfangen. Denn seine Lieblingsbeschäftigung ist es, Gruppen in ihre Bestandteile zu zerlegen und die weiter zu untersuchen. "Bestandteil" soll heißen Untergruppe: Das ist eine Teilmenge der Gruppe, die ihrerseits wieder Gruppe ist, das heißt zu jedem Element das Inverse, zu zwei Elementen deren Produkt und natürlich das neutrale Element enthält. Und die Ordnung, das heißt die Anzahl der Elemente, einer Untergruppe ist stets ein Teiler der Ordnung der ganzen Gruppe.

Also wissen wir schon ungefähr, wie viele Elemente eine Untergruppe der Ikosaedergruppe haben kann: Die Anzahl muss ein Teiler von 120 sein. Nun hat 120 sehr viele Teiler, entsprechend könnte es ein sehr reichhaltiges Sortiment von Untergruppen geben. Das gibt es in der Tat (was allerdings nicht schon aus der schlichten Anzahl 120 folgt), und deshalb findet ein Gruppenfreak an der Ikosaedergruppe reiche Beschäftigung. Die Menge aller Drehungen um eine bestimmte Achse, mitsamt den Spiegelungen, aus denen diese Drehungen zusammengesetzt sind, ist eine Untergruppe; und derlei Achsen gibt es 31 Stück.

Uns soll von all diesen Untergruppen nur noch eine näher interessieren: die so genannte Drehgruppe, die aus allen Drehungen, nicht aber Spiegelungen besteht. Das muss man etwas näher erläutern. (Wenn Sie lineare Algebra können, geht es ganz schnell. Jedes unserer Gruppenelemente entspricht einer 3x3-Matrix. Eine Spiegelung hat Determinante -1. Die Drehgruppe besteht aus allen Elementen mit Determinante +1.) Eine Spiegelung macht aus einer rechten Hand eine linke (und umgekehrt), und eine rechte Hand bleibt unter jeder Drehung eine rechte. Eine Abbildung aus der Ikosaedergruppe, die aus einer rechten Hand eine rechte macht, muss also aus einer geraden Anzahl von Spiegelungen bestehen. Nennen wir Abbildungen dieser Art "gerade" und die anderen "ungerade". Die Menge aller geraden Abbildungen ist eine Untergruppe (denn wenn zwei Abbildungen eine rechte Hand rechte Hand sein lassen, dann gilt das auch für ihre Zusammensetzung), und das ist die Drehgruppe des Ikosaeders. Sie hat genau 60 Elemente. Kurioserweise ist sie isomorph (strukturgleich) der alternierenden Gruppe A₅; das ist die Gruppe der Permutationen von fünf Elementen, die aus einer geraden Anzahl von Transpositionen (Zweiervertauschungen) bestehen. Das sieht man, wenn man sich die Ecken des Dodekaeders (die gleich den Spitzen des Tetraederfünflings sind, vergleiche Folge 12 "Durchdringungskörper") scharf genug anschaut. Es steht in "Regular polytopes" vom H. S. M. Coxeter, § 3.5 und 3.6; so ganz einfach ist es nicht.

Das war nun doch ein etwas längerer Ausflug in die Gruppentheorie. Was haben wir davon?
Zunächst eine saubere Definition der Polyederfamilie. Was ich bisher – nicht ganz präzise – als die Familie der Fünfzähligen bezeichnet habe, sind diejenigen geometrischen Gebilde, die unter der Symmetriegruppe des Ikosaeders invariant sind. Das heißt: Wenn man irgendeine Abbildung aus unserer Ikosaedergruppe auf das Ding anwendet, geht es in sich selbst über.

So wie die Symmetriegruppe des Ikosaeders zu den echten Fünfzähligen gehört, so gehört die kleinere Drehgruppe des Ikosaeders zu den "missratenen" Fünfzähligen, zu den Bastarden wie dem schiefen Dodekaeder oder dem Tetraederfünfling, die eben nicht spiegelsymmetrisch sind, sondern in einer linken und einer rechten Variante vorkommen. Je kleiner die Symmetriegruppe ist, desto weniger Bedingungen muss der Körper erfüllen, um unter der Symmetriegruppe invariant zu sein. Je "edler" der Körper, desto größer ist seine Symmetriegruppe, das heißt die Menge aller Abbildungen, die ihn invariant lassen.

Was ich am Beispiel der Fünfzähligen-Familie ausgeführt habe, gibt es für die Vierzähligen genauso. Die entsprechende Symmetriegruppe heißt üblicherweise Oktaedergruppe (obgleich man sie genauso gut Würfelgruppe nennen könnte). Sie hat 48 Elemente und entsteht dadurch, dass man alle Produkte von Spiegelungen um 9 verschiedene Ebenen bildet. Man sagt, diese Spiegelungen "erzeugen" die Gruppe. Neben zahlreichen Untergruppen gibt es die Drehgruppe des Oktaeders, die aus allen geraden Elementen der Oktaedergruppe besteht. Sie hat – wenig überraschend – 24 Elemente und ist – nicht ganz so selbstverständlich – isomorph zur Gruppe aller Permutationen von vier Elementen. Die Tetraedergruppe hat 24 Elemente, und die zugehörige Drehgruppe mit 12 Elementen ist isomorph zur alternierenden Gruppe A₄, das sind die geraden Permutationen von vier Elementen, die man in diesem Fall sogar mit den Ecken des Tetraeders identifizieren darf.

Dann kommen noch die unendlich vielen, aber nicht besonders erregenden Symmetriegruppen des n-seitigen Prismas für beliebige Werte von n. Sie bestehen aus n Drehungen um den n-ten Teil des Vollwinkels und Vielfache dieses Winkels, alle um ein und dieselbe Achse, plus dieselben Drehungen mitsamt einer Spiegelung. Plus – nicht zu vergessen – die Spiegelung an der Mittelebene, die die n-eckige Grundfläche des Prismas in dessen ebenfalls n-eckige Deckfläche überführt und umgekehrt.

Und das war's! Jede endliche Gruppe von Kongruenzabbildungen im Raum ist eine aus dem soeben aufgezählten Sortiment. Alle zusammen heißen Punktgruppen, weil sämtliche Elemente der Gruppe einen bestimmten Punkt, nämlich den Körpermittelpunkt, unverändert lassen. Insbesondere gibt es keine Translationen unter den endlichen Gruppen von Kongruenzabbildungen. Wäre nämlich eine Translation (Verschiebung um einen Vektor) dabei, dann müsste auch die Verschiebung um den doppelten Vektor dazugehören (das ist nämlich nur dieselbe Verschiebung zweimal hintereinander), und um den dreifachen, vierfachen, … Schon hätte die Gruppe unendlich viele Elemente.

Das war der analytische Teil: Wir haben zu einem gegebenen Körper die Symmetrieeigenschaften gefunden. Nicht nur zu Dodekaeder und Ikosaeder, bei denen ich das im Einzelnen vorgeführt habe, sondern bei allem, was man durch irgendwelche Manipulationen daraus machen kann: Entecken, Entkanten, Versternen, Durchlöchern – ich habe Ihnen ja in den vergangenen Folgen allerlei vorgeführt. Vorausgesetzt natürlich, die jeweilige Manipulation findet auf symmetrische Weise statt. Formal ausgedrückt: Erst entecken, dann verdrehen muss dasselbe ergeben wie erst verdrehen und dann entecken. Die beiden Operationen sind vertauschbar!

Die Symmetriegruppe erlaubt jedoch darüber hinaus auch die Erzeugung geometrischer Gebilde mit vorgegebenen Symmetrieeigenschaften. Aber davon erzähle ich Ihnen ausführlicher in der nächsten Folge.

Kommentare und Anregungen sind wie immer stets willkommen!

Herzlich Ihr

Christoph Pöppe
Redakteur bei Spektrum der Wissenschaft