Anscheinend spricht sich diese Serie allmählich in der Szene herum – was deren Autor natürlich erfreut –, und ich bekomme Rückmeldungen und Hinweise, die ich hiermit gerne weiterreiche. Reinhard Wolff, Waldorflehrer und Polyeder-Begeisterter, hat mir die Website "Polyhedra" genannt. Jeder platonische Körper passt ja auf – mehr oder weniger – symmetrische Weise in jeden anderen. Das Applet von Gian Marco Todesco setzt auf Knopfdruck zwei platonische Körper in Form von Drahtmodellen ineinander, dann den dritten innen in die beiden anderen, und so weiter; alle zusammen rotieren so, wie man es ihnen mit der Maus ansagt.

Ulrich Mikloweit, der Autor des Polyedergartens, den ich voll der Bewunderung Ihrer Aufmerksamkeit anempfahl, hat mich auf einen neuen großen, sehr hellen Stern am Polyederhimmel aufmerksam gemacht – am Südhimmel wohlgemerkt: Robert Webb ist aus Melbourne (Australien). Er hat das Thema Polyeder so richtig nach dem Herzen eines Mathematikers angepackt: sehr allgemein, schön abstrakt, sodass komplizierte Dinge auf einmal übersichtlich werden, und sehr vollständig. Herausgekommen ist ein Programm namens "Stella", das einer eierlegenden Wollmilchsau schon ziemlich nahe kommt. Grundausstattung ist ein reichhaltiges Sortiment von Polyedern; die platonischen und archimedischen, die ich Ihnen beschrieben habe, samt ihren Dualen sind dabei, und noch viel mehr. Dazu kommt ein reichhaltiger Werkzeugkasten, mit dem man ein Polyeder nicht nur analysieren, sondern auch auf viele Weisen verwandeln kann. Dadurch entsteht eine unglaubliche Vielfalt neuer Körper. Für Leute wie mich, die sich die Dinger auch handgreiflich aus Karton bauen möchten, gibt es das jeweilige Polyeder aufgeschnitten und in der Fläche ausgebreitet, sodass man sich Bastelbögen zurechtmachen kann.

Aus den vielen schönen Dingen, die in Robert Webbs "Stella" zu finden sind, greife ich diesmal nur das heraus, was der ganzen Sache den Namen gegeben hat. Über etliche andere wird in späteren Folgen zu berichten sein.

Der Name "Stella" ist verkürzt aus stellation; das wiederum ist aus dem lateinischen Wort stella für "Stern" abgeleitet, wäre also ungefähr als "Versternung" zu übersetzen. In der Tat macht eine Stellation aus manchen Körpern Sternkörper, wie ich sie in Folge 9 beschrieben habe: Man setze auf jede Seitenfläche des Körpers ein Pyramidchen oder "Zelt" und fahre die Zeltstange in der Mitte genau so weit aus, dass es gut aussieht. Aber das Prinzip ist anders. Bei einer Stellation entstehen die Zeltwände dadurch, dass die benachbarte Seitenfläche des ursprünglichen Polyeders ausgedehnt wird. Beim Dodekaeder wird aus jedem Fünfeck ein Fünfstern (Pentagramm), und die neu hinzugekommenen Spitzen des Fünfsterns bilden zusammen die Zelte.

Jetzt lassen wir die mathematische Allgemeinheit zu ihrem Recht kommen: Wir nehmen uns ein Ur-Polyeder her (das Dodekaeder ist ein gutes Beispiel) und schauen uns die Ebenen an, die durch seine Seitenflächen gebildet werden. Das sind zwölf Stück im Falle des Dodekaeders. Sie sind paarweise parallel, aber im Übrigen schneiden sie sich. Wenn man sich jetzt den gesamten Raum als großen Käse vorstellt (als unendlich großen Käse, wohlgemerkt) und jede Ebene als ein Käsemesser, das diesen Raum in zwei Teile zerlegt, dann haben wir es hinterher mit einer ganzen Menge von – na ja, nicht gerade Käsewürfeln, aber immerhin Käsestücken zu tun. Einige davon, die ganz außen liegen, gehen bis unendlich; da sie ziemlich unhandlich sind, lassen wir sie weg und kümmern uns nur um die endlichen Stücke.

Das kleinste, innerste unter ihnen ist das ursprüngliche Polyeder. Darum gruppieren sich die Zelte, die das Ding zum Stern machen; und dann? Dann ist im Allgemeinen noch lange nicht Schluss. Beim Dodekaeder kommen als nächstes tetraederförmige "Keile", die die Lücken zwischen den Sternspitzen zustopfen. Das Ergebnis ist nicht besonders sternförmig. Erst die Käsestücke der nächsten Sorte haben wieder lange Spitzen (und Unterseiten, die genau in die Vertiefungen des Vorgängerkörpers passen) und machen einen großen, sehr spitzen Stern.

Es gibt also nicht nur eine Stellation des Dodekaeders, sondern deren drei. Die Kurzfilme auf dieser Seite führen sie Ihnen eine nach der anderen vor. Die Endergebnisse jeder Stellation sind gute Bekannte: kleines Sterndodekaeder, großes Dodekaeder, großes Sterndodekaeder.

Dazu eine kleine persönliche Geschichte (wenn's Sie nicht interessiert: Am Anfang des nächsten Absatzes geht's weiter). Das kleine Sterndodekaeder muss mir schon über den Weg gelaufen sein, als ich zwölf Jahre alt war. Jedenfalls kam es mir als geeignete Form in den Sinn, als wir im Kunstunterricht in der 7. Klasse eine St.-Martins-Laterne zu bauen hatten. In die Seitenflächen des Sterns schnitt ich möglichst wohlgeformte Löcher und klebte farbiges Transparentpapier dahinter, wie man das so macht. Fiffi (so hieß unser Kunstlehrer mit Spitznamen) war ziemlich beeindruckt und obendrein erleichtert, mir wenigstens dafür eine gute Note geben zu können. Ansonsten waren meine Malkünste eher als mangelhaft zu bewerten (was sich bis heute leider nur unwesentlich gebessert hat). So kam ich an meine Drei in Kunst. Es war die letzte Kunstnote meines Lebens (Lehrermangel, Kunst abgewählt, ...) und wurde deswegen in mein Abiturzeugnis übernommen. Also hat mich meine frühe Neigung zu Polyedern vor einem Schandfleck auf dem Reifezeugnis bewahrt. Na gut.

Wie sieht es mit den Stellationen der anderen platonischen Körper aus? Bei Tetraeder und Würfel ziemlich uninteressant. Nach der großen Messerschneiderei bleibt, von dem ursprünglichen Körper abgesehen, nichts als unendlicher Käse übrig. Zum Oktaeder gibt es, immerhin, die acht Tetraederchen, die es zur Stella octangula ergänzen, und das war's schon. Nett, aber nicht neu. Das Dodekaeder liefert die oben beschriebenen drei Stellationen.

Aber das Ikosaeder! Da wird die Sache hoffnungslos unübersichtlich. Wie kommt das? Die Winkel zwischen benachbarten Flächen des Ikosaeders sind ziemlich stumpf. Es gibt wieder Paare paralleler Flächen; man nehme eine Fläche und statt ihrer parallelen Kollegin eine von deren unmittelbaren Nachbarinnen. Diese beiden Flächen sind nicht parallel, aber die Abweichung ist, wegen der stumpfen Flächenwinkel, nicht groß. Die zugehörigen Ebenen schneiden sich also erst ziemlich weit draußen. Das produziert großen, aber endlichen Käse. Vor allem werden diese großen, endlichen Käsestücke noch durch zahlreiche andere Ebenen durchschnitten (immerhin gibt es insgesamt 20 Ebenen).

Es ist schwierig, in diesem Käse den Überblick zu behalten. Die Fachleute haben sich anscheinend darauf geeinigt, dass es 59 verschiedene Stellationen des Ikosaeders gibt. Aber da gibt es Interpretationsmöglichkeiten.

Was genau soll man eine Stellation nennen? Der radikale, ganz abstrakte Standpunkt wäre: Hier ist eine (ziemlich große) Zahl endlicher Käsestücke in einer bestimmten Anordnung. Jede Teilmenge dieser Gesamtmenge nenne ich eine Stellation des Ikosaeders (wobei natürlich jedes zur Teilmenge gehörige Teilstück an seinem Platz bleiben muss). Das schließt nicht aus, dass eine Stellation aus mehreren völlig getrennten Teilstücken besteht. In einigen Spezialfällen hat das einen gewissen Reiz; aber meistens möchte man diese zerbröselten Körper nicht mitzählen und besteht darauf, dass das Ding zusammenhängend ist. (Wobei man sich wieder darüber streiten kann, ob zwei Teile, die nur einen Eckpunkt gemeinsam haben, schon als zusammenhängend gelten sollen oder ob dafür Zusammenhang entlang einer Kante oder gar Fläche erforderlich ist.)

Schlimmer noch: Unter die Definition mit der schlichten Teilmenge fällt zum Beispiel eine ungestalte Zusammensetzung aus Dodekaeder, ein paar Pyramidchen nach Belieben und ein paar Keile drauf, ebenfalls nach Belieben. Da regt sich dann doch der Standesdünkel der Platonischen: Aus der Familie sollte der durch Stellation erweiterte Körper schon sein! Das heißt, die Symmetrie des Urkörpers sollte erhalten bleiben.

Das wiederum heißt: Alle Ebenen sind gleich zu behandeln, wenn der Urkörper ein platonischer ist. Allgemeiner sind die Ebenen, die zu gleichartigen Flächen gehören, gleich zu behandeln. Also greift man sich aus jeder Gruppe gleichartiger Ebenen einen Stellvertreter heraus und betrachtet den genauer. Bei platonischen Körpern und insbesondere beim Ikosaeder läuft das darauf hinaus, genau einen Ebenentyp zu betrachten.

Hier ist eine der zwanzig Ebenen des Ikosaeders. Eingezeichnet sind die Geraden, in denen die übrigen Ebenen unsere Beispielebene schneiden. Sie zerlegen die Ebene in Teilflächen, von denen einige bis ins Unendliche ragen und uns deswegen nicht weiter interessieren. Das kleine Dreieck ganz in der Mitte ist die Ikosaederfläche selbst. Für jede der (endlichen) Teilflächen kann man nun entscheiden, ob sie mit zur jeweiligen Stellation gehören soll oder nicht – allerdings unter Beachtung der Symmetrievorschriften. Es würde dem Familiensinn der Fünfzähligen widersprechen, wenn man von drei Teilflächen, die durch eine Dritteldrehung um den Mittelpunkt des Schemas ineinander übergehen, eine mitnehmen und die beiden anderen weglassen würde.

Muss man auch zwei Teilflächen gleich behandeln, die Spiegelbilder voneinander sind (bezüglich einer Achse, die durch den Mittelpunkt des Schemas geht)? Na ja, ganz strenggenommen schon. Aber bei der Spiegelsymmetrie war man ja schon bei anderer Gelegenheit nicht ganz so streng. So wurde das schiefe Dodekaeder – mehr oder weniger zähneknirschend – als Bastard am Tisch der Fünfzähligen geduldet. Und die Durchdringung von fünf Tetraedern sowieso; dem Charme der Asymmetrie – diesem hübsch-frechen Dreh – könnten sich auch die Gestrengen nicht entziehen. Und siehe da: Der Tetraederfünfling findet sich unter den Stellationen des Ikosaeders wieder.

Am Beispiel des Ikosaeders haben wir's gesehen: Eine Stellation ist um so ergiebiger, je mehr Flächen der Ursprungskörper hat. Reiche Beute versprechen daher die kugelähnlichen archimedischen Körper sowie eine Gruppe von Polyedern, von denen ich Ihnen noch nichts erzählt habe, weil sie sowieso ein Thema für sich sind: die uniformen Polyeder.

Ein eher biederer Körper kommt auf diese Weise zu neuen Ehren: das Rhombentriakontaeder (der Rhombendreißigflächner), das aus dem Dodekaeder entsteht, indem man jedem Fünfeck ein Zelt aufsetzt und die Zeltstange solange ausfährt, bis zwei entlang einer Kante benachbarte Dreiecke sich zu einer Raute verbinden (vergleiche Folge 9). Peter W. Messer hat in der Veröffentlichung "Stellations of the rhombic triacontahedron and beyond" das Stellationsschema des Rhombentriakontaeders wiedergegeben. Es ist noch weit komplizierter als das des Ikosaeders; und unter diesen Stellationen findet sich, neben vielen anderen, die der unermüdliche Magnus Wenninger gebaut hat, ein echter Prachtkörper, der Fünffachwürfel (siehe Folge 12 "Durchdringungskörper").

Robert Webb, in seinem Bestreben nach möglichst großer Allgemeinheit, möchte auch Körper der Stellation unterziehen (wahrscheinlich heißt das Verb "stellieren"), die vielleicht hohl oder sonstwie merkwürdig geformt sind. Bei ihm geht eine Stellation deswegen nicht unbedingt nach außen (und manchmal ist der Begriff "außen" auch schlecht definiert). Deswegen nimmt er einen relativ radikalen Standpunkt ein: Zwei Polyeder A und B heißen Stellationen voneinander, wenn ihre Flächen in denselben Ebenen liegen. Oder mathematisch fomuliert: wenn es zu jeder Fläche von A eine Fläche von B gibt, die in derselben Ebene liegt, und umgekehrt. Dann ist eben auch das (Standard-)Dodekaeder eine Stellation des kleinen Sterndodekaeders – etwas gewöhnungsbedürftig, da es sich eher um eine Entsternung als eine Versternung handelt. Aber das Unbehagen gibt sich.

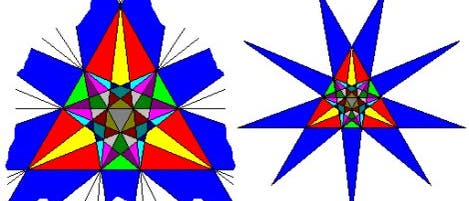
Die Ergebnisse sind jedenfalls recht eindrucksvoll. Die vier Beispiel auf dieser Seite stammen aus der ausführlichen Beschreibung des Programms "Stella" von Robert Webb.

Kommentare und Anregungen sind wie immer stets willkommen!

Herzlich Ihr

Christoph Pöppe
Redakteur bei Spektrum der Wissenschaft

Literatur zu dieser Folge:
Die Stellation des Ikosaeders gibt viele hübsche Bilder. Da haben sich etliche Webautoren nicht lumpen lassen, zum Beispiel Steven Dutch, den wir von den unendlichen Polyedern schon kennen:
www.uwgb.edu/dutchs/symmetry/stelicos.htm
oder der Mathematica-Autor Roman Mäder:
www.mathconsult.ch/showroom/icosahedra
oder Guy Inchbald, der noch Neues zur Theorie beigetragen hat:
Towards stellating the icosahedron and faceting the dodecahedron. New findings on stellation, faceting and untidy polyhedra.
http://www.steelpillow.com/polyhedra/icosa/stelfacet/StelFacet.htm
Ein bereits deutlich allgemeinerer Standpunkt (samt Stellation eines eher weniger populären Polyeders) wird vertreten in:
J. L. Hudson, J. G. Kingston: Stellating Polyhedra. The Mathematical Intelligencer Bd. 10, No. 3, S. 50-61 (1988).
Peter W. Messer: Stellations of the rhombic triacontahedron and beyond / Les étoilements du rhombitriacontaèdre et plus. Structural topology / Topologie structurale Bd. 21, S. 25 – 46 (1995).