Während meiner Forscherkarriere habe ich nicht in der reinen Mathematik gearbeitet. Mein Thema ist die mathematische Astronomie: die Anwendung der Mathematik auf die Bewegung der Himmelskörper. Und wie immer, wenn die abstrakte Mathematik es mit der realen Welt zu tun bekommt, muss man Abstriche machen. Die gravitative Wechselwirkung von mehr als zwei Objekten lässt sich mathematisch nicht exakt lösen. Wenn ich in der Astronomie trotzdem über die Bewegung von Planeten und Asteroiden im Sonnensystem Bescheid wissen will, muss ich mich mit Näherungslösungen begnügen. Der Unterschied zwischen Theorie und Realität lässt sich aber trotzdem mathematisch ausdrücken:

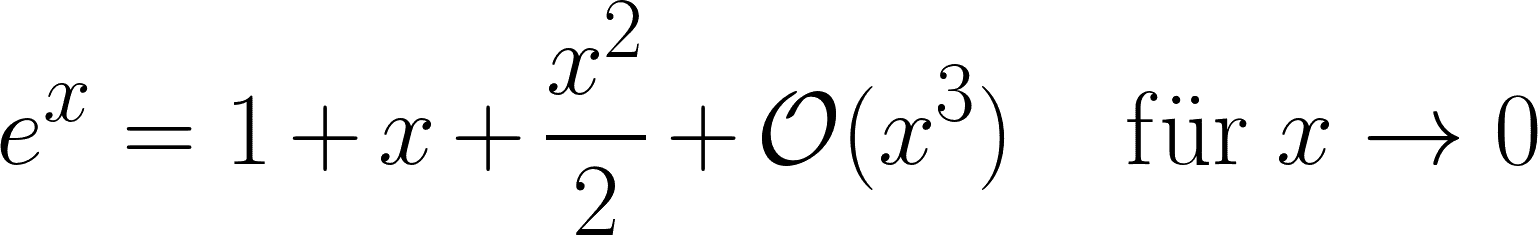
Diese Formel ist ein typisches Beispiel. Sie zeigt die Reihenentwicklung der Exponentialfunktion. Eine mathematische Funktion kann unter gewissen Bedingungen auch als unendliche Summe dargestellt werden. In der Realität kann man aber natürlich nicht unendlich viele Additionen durchführen, sondern muss die Berechnung nach einer bestimmten Zeit abbrechen. Mit dieser Taktik kann man exakt unlösbare Gleichungen näherungsweise lösen, macht aber zwangsläufig einen Fehler. Wie groß dieser Fehler ist, zeigt uns in diesem Beispiel der letzte Term am Ende der Formel.

Das »O« am Ende ist ein so genanntes »Landau-Symbol«. Verwendet hat es erstmals der deutsche Mathematiker Paul Bachmann im Jahr 1894, bekannt gemacht aber sein Kollege Edmund Landau, nach dem es auch benannt wurde. Man beschreibt damit, wie sich Funktionen und Folgen im Unendlichen verhalten. In unserem Beispiel haben wir die Reihenentwicklung nach drei Termen abgebrochen. Statt der eigentlich unendlichen Summe berechnen wir nur 1 + x + x²/2 und ignorieren alle restlichen Ausdrücke, die noch folgen würden. Ignorierten wir den Rest aber tatsächlich, dann dürften wir in der Formel auch kein Gleichheitszeichen verwenden, denn die Exponentialfunktion ist mit Sicherheit nicht gleich 1 + x + x²/2.

Man kann den Fehler, den man durch die Näherung macht, aber abschätzen. In der Reihenentwicklung tauchen immer höhere Potenzen von x auf, und wenn die Zahl x, für die wir die Funktion berechnen, ausreichend klein ist, sind auch die jeweiligen Potenzen immer klein. Oder anders gesagt: Wir können uns sicher sein, dass der Fehler der Näherung nie größer wird als ein Ausdruck der Ordnung x³. Genau das besagt das entsprechende Landau-Symbol, und wenn wir es in die Formel mit aufnehmen, wird unsere Gleichung wieder korrekt.

Zu wissen, wie sich eine Folge oder Funktion im Unendlichen verhält, auch wenn man es nicht konkret ausrechnen kann, ist vor allem in der Informatik wichtig. Während meiner Doktorarbeit musste ich viele Computerprogramme schreiben, die numerisch die gravitative Wechselwirkung zwischen einer gewissen Anzahl von Himmelskörpern berechnen. Bei nur drei Objekten muss man insgesamt sechs Wechselwirkungen kalkulieren. Bei vier Himmelskörpern steigt die Zahl der zu berechnenden Wechselwirkungen auf 12 – und so weiter, denn allgemein existieren für n Objekte n²-n gravitative Wechselwirkungen, die man berechnen muss (den gravitativen Einfluss eines Objekts auf sich selbst kann man ignorieren, deswegen zieht man von n² noch einmal n ab).

Unter Verwendung der Landau-Symbole kann man sagen, dass die Zahl der Rechenoperationen für n Himmelskörper mit O( n²) steigt. Das ist kein Problem, wenn n klein ist. Aber wenn man es mit vielen Objekten zu tun hat (zum Beispiel den Milliarden Sternen einer Galaxie), wird der Aufwand schnell unpraktisch groß. Aber mit ein paar kreativen mathematischen Tricks kann man die Zahl der Rechnungen unter Umständen reduzieren. Der Algorithmus, den ich für meinen speziellen Fall am Ende entwickelt habe, verhielt sich nicht mehr wie O( n²) sondern wie O(log n). Ein auf den ersten Blick unspektakulärer, aber in der Praxis sehr wichtiger Erfolg!