In einem alten Buch über Mathematik habe ich kürzlich folgende Formel entdeckt:

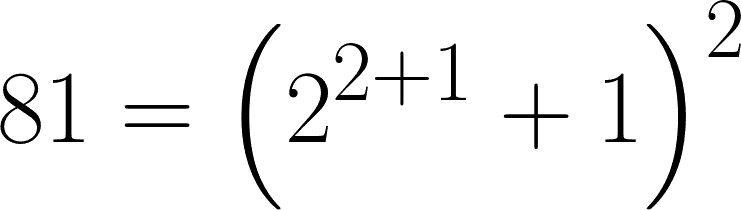
Sie fiel mir wegen ihrer scheinbaren Sinnlosigkeit auf. Das war keine »echte« Formel, sondern einfach nur eine Rechnung. Eine unnötig komplizierte noch dazu, obwohl sie korrekt ist, wie man ja leicht überprüfen kann. Nun wollte ich natürlich wissen, was sie in einem Buch mit dem Titel »Wonders of Numbers« (Clifford Pickover, Oxford University Press) zu suchen hat. Welche mathematischen »Wunder« verbergen sich hinter der seltsamen Berechnung?

Der Autor beschäftigt sich im entsprechenden Kapitel mit »Kreationszahlen«. Die definiert er als die kleinste Anzahl an Ziffern, die benötigt werden, um eine bestimmte, in diesem Fall ganze Zahl zu konstruieren. Die Aufgabe bestand darin, nur unter Verwendung der Ziffern »1« und »2« und der Rechenoperationen Addition, Subtraktion, Multiplikation und Exponentation eine vorgegebene Zahl zu bilden und dabei möglichst wenige Ziffern zu verwenden. Im Fall der oben gezeigten Formel wäre die Kreationszahl für 81 also gleich 5, da man fünf Ziffern (je einmal die 2 und die 1 und dann noch einmal 2, 1 und 2 beim Potenzieren) braucht. Oder genauer gesagt: Die Kreationszahl für 81 ist kleiner oder gleich 5, denn es wurde mit dieser einen Rechnung nicht streng bewiesen, dass es nicht auch mit weniger Ziffern möglich ist, die 81 zu bilden.

In einem Forum rief der Autor damals den »Creator Numbers Contest« ins Leben. Die Zahlen 20, 120 und 567 sollten mit so wenigen Ziffern wie möglich dargestellt werden. Im letzten Fall bestand eine der ersten eingereichten Konstruktionen aus der Rechnung 567 = 2 · 2 · [(2 · (2 · 2 + 2))² – 2] – 1. Achtmal die Ziffer 2 und einmal die 1, woraus sich eine Kreationszahl von 9 ergibt.

Doch es geht noch besser, wie sich im Lauf des Wettbewerbs zeigte: Bei der Rechnung 567 = (2^{2 + 2 + 2} – 1) · (2 + 1)² werden nur acht Ziffern benötigt. Die Teilnehmerinnen und Teilnehmer hatten schnell entdeckt, dass die Vorgaben des Wettbewerbs die Verwendung mehrstelliger Zahlen nicht explizit ausschließen – und so Konstruktionen wie diese hier ermöglichen: 567 = (2 + 1)^2 + 1 · 21, die nur sechs Ziffern benötigt. Eine noch sparsamere Rechnung wurde aber nicht gefunden, und die Kreationszahl von 567 konnte nicht mehr weiter gesenkt werden.

Die Lösungen des »Creator Numbers Contest« wurden im Allgemeinen durch Ausprobieren gefunden; einige engagierte Mathematiker verfassten sogar komplexe Computerprogramme, die Berechnungen automatisiert erstellten und prüften, und stießen dabei auf weitere Möglichkeiten der Konstruktion, etwa durch die Verwendung negativer Exponenten. Die Zahl 567 ließe sich dann auch mit der Rechnung

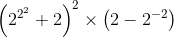
konstruieren. In diesem Fall erhält man damit zwar keine kleinere Kreationszahl als bei der vorherigen Rechnung; bei anderen Zahlen lässt sich die Kreationszahl durch den kreativen Einsatz negativer Exponenten jedoch durchaus senken. Und warum hier aufhören? Man kann statt ganzzahliger Exponenten auch gebrochene verwenden und damit sogar irrationale Zahlen konstruieren. Ob das aber dabei hilft, die Kreationszahlen auch von ganzen Zahlen zu senken, bleibt unbeantwortet.

Die Beschäftigung mit den Kreationszahlen ist zugegebenermaßen eher Unterhaltung und keine Forschung. Allein die Tatsache, dass eine so simple Aufgabenstellung im Rahmen des »Creator Numbers Contest« Menschen dazu motiviert hat, sich derart ausführlich mit dem Problem zu beschäftigen, zeigt allerdings, dass die ganze Angelegenheit nicht ohne Wert ist. Und dass in der Mathematik einfache »Spielereien« sehr schnell sehr komplex werden können. Wer weiß, vielleicht finden die Kreationszahlen irgendwann doch noch ihren Platz in der »echten« Mathematik.