Gerade m, die auf einer Strecke \(\overline{AB}\) senkrecht steht und diese halbiert, also durch den Mittelpunkt von \(\overline{AB}\) verläuft.

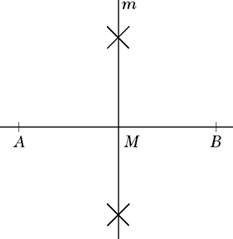
Um die Mittelsenkrechte einer Strecke \(\overline{AB}\) zu konstruieren, werden um beide Endpunkte dieser Strecke Kreise mit gleich langen Radien, die länger sind als die halbe Länge der Strecke \(\overline{AB}\), gezeichnet. Diese beiden Kreise haben zwei Schnittpunkte, deren Verbindungsgerade m die Mittelsenkrechte der Strecke \(\overline{AB}\) ist.

Die Konstruktionsvorschrift für die Mittelsenkrechte kann auch angewendet werden, um den Mittelpunkt M einer gegebenen Strecke zu bestimmen, welcher sich als Schnittpunkt der Strecke mit der Mittelsenkrechten ergibt.

In jedem beliebigen Dreieck ABC schneiden sich die Mittelsenkrechten (auch Dreieckstransversalen genannt) der drei Dreieckseiten in einem Punkt, dem Mittelpunkt des Umkreises.