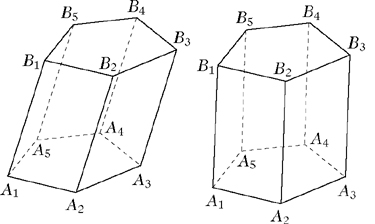
ebenflächig begrenzter Körper mit zwei kongruenten, in parallelen Ebenen liegenden n-Ecken A₁A₂ …A_n und B₁B₂ …B_n als Grund- und Deckfläche, sowie n Parallelogrammen als Seitenflächen.

Die beiden n-Ecke müssen „parallelkongruent“ zueinander sein, d. h., sie müssen durch eine Verschiebung auseinander hervorgehen; die Eckpunkte der Parallelogramme sind jeweils zwei Paare zueinandergehörender Ecken der Grund- und Deckfläche. Die Seiten der Grund- und Deckfläche heißen Grundkanten, diejenigen der Seitenflächen Mantellinien des Prismas. Ein Prisma, dessen Grund- und Deckfläche jeweils n Ecken haben, besitzt somit 3n Kanten, davon n Mantellinien, und wird n-seitiges Prisma genannt.

Verlaufen die Mantellinien eines Prismas senkrecht zur Grundfläche, so heißt es gerades Prisma, anderenfalls schiefes Prisma. Als Höhe eines Prismas wird der Abstand der beiden Ebenen, denen die Grund- und die Deckfläche angehören, bezeichnet. Das Volumen eines Prismas hängt aufgrund des Prinzips des Cavalieri (Cavalieri, Prinzip des) nur von der Höhe h und vom Flächeninhalt A_G der Grundfläche ab, nicht jedoch davon, ob es sich um ein gerades oder schiefes Prisma handelt; es gilt in beiden Fällen V = A_G ·h. Ein Prisma, dessen Grundund Deckfläche regelmäßige Vielecke sind, heißt regelmäßiges Prisma; sind Grund- und Deckfläche eines Prismas Parallelogramme, so handelt es sich um ein Parallelepiped.