Lexikon der Mathematik: Wurzelfunktion
die Funktion
die jeder nichtnegativen Zahl x ihre nichtnegative (reelle) Wurzel, also die eindeutig existierende Zahl y ∈ [0,∞) mit y2 = x, zuordnet. Die Wurzelfunktion ist streng isoton, stetig und in (0,∞) differenzierbar mit
Allgemeiner heißt für k ∈ ℕ die Funktion
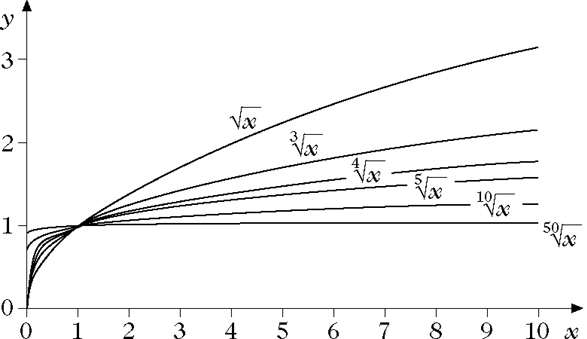
die jeder nichtnegativen Zahl x ihre nichtnegative k-te Wurzel, also die eindeutig existierende Zahl y ∈ [0,∞) mit yk = x, zuordnet, k-te Wurzelfunktion.
Auch die k-te Wurzelfunktion ist streng isoton, stetig und in (0,∞) differenzierbar mit
Mit Hilfe der Potenzfunktion läßt sie sich schreiben als \(\sqrt[k]{x}={x}^{1/k}\).
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.