Lexikon der Physik: Heterostrukturen
Heterostrukturen
Nikolaus Nestle, Regensburg
Karl Eberl, Stuttgart
Unter Heterostrukturen oder Halbleiterheterostrukturen versteht man monokristallin aufeinander gewachsene Schichten von Halbleitern unterschiedlicher Zusammensetzung ( Abb. 1 ). Solche Schichtstrukturen zeigen eine Fülle von interessanten und technisch relevanten Quantisierungseffekten bezüglich ihrer elektronischen und optischen Eigenschaften und stellen eine wichtige Basis für die Herstellung neuartiger mikroelektronischer Bauelemente dar. Die wichtigste Materialkombination für die Herstellung von Halbleiterheterostrukturen ist das System GaAs/AlGaAs.
Herstellung
Halbleiterheterostrukturen sind thermodynamisch im allgemeinen nicht stabil (Verzicht auf Mischungsentropie!) und müssen deshalb mit speziellen Epitaxieverfahren (Epitaxie) hergestellt werden, die außerhalb des thermodynamischen Gleichgewichts arbeiten. Die wichtigsten derartigen Verfahren sind die Molekularstrahlepitaxie (MBE), die chemische Gasphasenabscheidung (CVD) und die Flüssigphasenepitaxie (LPE).
Eigenschaften
Die wohl interessanteste Eigenschaft von Halbleiterheterostrukturen ist die Ausbildung von Quantenfilmen an Grenzflächen verschiedener Materialien. Diese entstehen auf Grund der unterschiedlichen Energieverhältnisse in den beiden Materialien und weil die Fermi-Energie der Ladunsgträger in allen miteinander in Kontakt befindlichen Materialien den gleichen Wert besitzen muß ( Abb. 2 ). Die so vorgegebene Energieverteilung hat zur Folge, daß sich Ladungsträger aus der Umgebung (›Barriere‹) im Quantenfilm sammeln.
Dort sind sie dann in ihrer Bewegunsgfreiheit weitgehend auf die Schicht eingeschränkt und bilden ein zweidimensionales Elektronengas (2DEG) bzw. ein 2D-Löchergas. Die Einschränkung der Ladungsträgerbewegung auf zwei Dimensionen kommt dadurch zustande, daß sich die Elektronen senkrecht zur Schicht in einem Potentialtopf befinden, in dem ihnen nur bestimmte quantisierte Energiezustände zur Verfügung stehen ( Abb. 3 ). Die Bewegungsfreiheit der Elektronen in der Schicht wird durch diese Quantisierung nicht beeinträchtigt (Separation der Wellenfunktionen).
Im Gegensatz zum dreidimensionalen Fall ist die Zustandsdichte der Elektronen in Abhängigkeit von ihrer Bewegungsenergie (Dispersionsrelation) innerhalb des 2DEGs konstant. Wenn man ein 2DEG in ein Magnetfeld bringt, so bewirkt die Magnetfeldkomponente senkrecht zur Schicht eine weitere Quantisierung der Elektronenbewegung (Landau-Niveaus), die im halbklassischen Bild einer Festlegung der Elektronen auf Zyklotronbahnen entspricht. Durch diese Quantisierung kommt es zur Verteilung der Elektronenenergien auf einige wenige diskrete Werte mit makroskopischen Besetzungszahlen. Dies hat unter anderem besonders ausgeprägte Magnetowiderstandserscheinungen beim Quanten-Hall-Effekt und beim Schubnikow-de Haas-Effekt zur Folge. Die hohen Elektronenbeweglichkeiten in 2DEGs in Halbleiterheterostrukturen erlauben nicht nur die besonders gute Beobachtung von derartigen Quantisierungseffekten, sondern sind auch eine wichtige Voraussetzung für die Herstellung von besonders schnellen Halbleiterbauelementen für Höchstfrequenzanwendungen (z.B. High Electron Mobility Transistor, HEMT).
In Halbleiterheterostrukturen mit vielen periodisch angeordneten Schichten, den sogenannten Übergittern ( Abb. 1 ), entstehen noch weitere Quantisierungserscheinungen: Soweit die Schichtperiode in der Größenordung der Elektronen-Wellenlänge liegt, kommt es in Wachstumsrichtung (also senkrecht zu den Schichten) zur Ausbildung einer speziellen Energieniveau-Struktur der Elektronen, den sog. Minibändern. Bei dickeren Schichten im Bereich von typischen Lichtwellenlängen verhalten sich die Schichten als wellenlängenselektive Spiegel (›Bragg-Spiegel‹) mit einem sehr hohen Reflexionsvermögen im Resonanzfall ( Abb. 4 ).
Anwendungen
Die im vorangehenden Abschnitt vorgestellten Eigenschaften von Heterostrukturen werden vielfach bereits technisch genutzt oder bilden zur Zeit die Grundlage für das Design neuer Halbleiterbauelemente. Die Quantisierung der Elektronenenergie in Quantenfilmen erlaubt beispielsweise die Steigerung des Wirkungsgrads von Leuchtdioden und Halbleiterlasern, die Bragg-Spiegel bilden z.B. die Funktionsgrundlage des Vertical Cavity Surface Emitting Lasers (VCSEL, Abb. 4 ).
Weitere Effekte mit interessanten Anwendungsmöglichkeiten für Halbleiterheterostrukturen ergeben sich durch die Möglichkeiten zur lateralen Mikrostrukturierung solcher Systeme (beziehungsweise des in ihnen enthaltenen 2D Elektronengases). Diese ist unter anderem durch verschiedene Ätzverfahren (z.B. Plasma-Ätzen oder naßchemische Verfahren), durch Ionenimplantation und durch das Aufbringen von sogenannten ›Gate‹-Elektroden möglich. Auf diese Weise kann das in der Grenzfäche enthaltene Elektronensystem noch weiter auf eine Dimension (›Quantendraht‹) oder gar auf ein kleines, in alle Raumrichtungen beschränktes Volumen (›Quantenpunkt‹) eingeschränkt werden. Dadurch kommt es dann zu zusätzlichen Quantisierungserscheinungen (z.B. Abb. 5 ), die eine Veränderung der Zustandsdichten bewirken und wiederum auch für die Realisierung neuartiger elektronischer und optoelektronischer Bauelemente genutzt werden können, beispielsweise für sogenannte Einzelelektrontransistoren ( Abb. 6 : Aufbau und ›Kennlinie‹), bei denen das Zusammenspiel von Quantisierunsgeffekten und elektrischer Abstoßung zwischen den Elektronen ausgenutzt wird. Derzeit funktionieren diese Einzelelektronenbauelemente aber nur bei tiefen Temperaturen. Für einen Einsatz bei Raumtemperatur müssen die Strukturen noch weiter verkleinert werden, dann erst wird die Energie der Coulomb-Blockade so groß, daß die Elektronen sie nicht mehr durch das thermische Rauschen überwinden können.
Perspektiven
Überwachsen vorstrukturierter Substrate
Die Wachstumsgeschwindigkeit von Schichten in der MBE ist für verschiedene Kristallrichtungen verschieden groß. Dieser Sachverhalt kann zur Herstellung von lateral strukturierten Quantenfilmen besonders hoher Qualität genutzt werden, für deren Herstellung man von einem bereits zuvor strukturierten Substrat ausgeht ( Abb. 7 ).
Selbstordnende Quantenpunkte
Bei der Epitaxie von stark verspannten Heterostrukturen kommt es beim Überschreiten bestimmter kritischer Lagendicken zur Bildung von Clustern (Stranski-Krastanov-Wachstum). Unter günstigen Umständen ergeben sich dabei selbstordnende Quantenpunkte von fast gleicher Größe ( Abb. 8 ). Diese eröffnen neue Möglichkeiten vor allem zur Herstellung von optoelektronischen Bauelementen. Auf dieser Basis hergestellte Halbleiterlaser könnten noch höhere Wirkungsgrade aufweisen wie die derzeit verfügbaren.
Neue Materialsysteme
Die Herstellung von Halbleiterheterostrukturen guter Qualität erfordert für jede einzelne Materialkombination besondere Forschungs- und Optimierungsanstrengungen, die um so schwieriger werden, je größer die Gitterfehlanpassung zwischen den beteiligten Materialien ist, und bei verschiedenen Gleichgewichtskristallstrukturen noch zusätzlich erschwert werden. Gerade solche Materialsysteme sind jedoch heute von ganz besonderem Interesse:
• Heterostrukturen aus GaAs und Phosphiden bzw. InP und Arseniden; solche Materialien werden vor allem für neue optoelektronische und nachrichtentechnische Bauelemente untersucht.
• Heterostruktruren aus Legierungen von Si, Ge und C.
• Heterostrukturen aus GaN und anderen Nitriden; diese Materialien sind zur Zeit vor allem für Leuchtdioden im blauen Spektralbereich von Interesse; sie kristallisieren jedoch im Gegensatz zu den meisten anderen technisch genutzten Halbleitern im hexagonalen System und haben außerdem eine deutlich kleinere Gitterkonstante als die anderen III-V-Halbleiter.
• II-VI-Halbleiter, vor allem Materialien auf ZnSe-Basis. Diese Materialklasse stellt einen zweiten Zugang zur Herstellung von guten ›blauen‹ Optobauelementen dar. Ein zusätzliches Problem bei dieser Materialklasse ist die hohe Giftigkeit einiger Ausgangsstoffe (Be, Cd, Se).
Schließlich sei noch angemerkt, daß in den letzten Jahren auch definierte Heterostrukturen aus metallischen Materialien immer größere Bedeutung erlangt haben, vor allem auch auf Grund ihrer ungewöhnlichen Magnetowiderstandseigenschaften (Riesenmagnetowiderstand). Die Schichtdicken, ab denen Quantisierungseffekte auftreten, sind hier oft noch kleiner als bei den Halbleitern und betragen nur wenige Atomlagen.
Literatur:
M. Jaros: Physics and applications of semiconductor microstructures, Oxford:Clarendon, 1989.
T. Ando, A.B. Fowler, F. Stern, Reviews of Modern Physics54 437, 1982.
M.J. Kelly, Low-Dimensional Semiconductors - Materials, Physics, Technology, Devices, Oxford: Clarendon, 1995.

Heterostrukturen 1: Transmissionselektronenmikroskopische Aufnahme einer Halbleiterheterostruktur (abwechselnde Schichten von GaAs und AlAs). Man erkennt die Fortsetzung des Kristallgitters über die Materialgrenzen hinweg. Eine Folge mit vielen periodisch angeordneten Schichten unterschiedlicher Halbleitermaterialien wird auch als Übergitter bezeichnet.

PTR>Heterostrukturen 2: Potentialverlauf mit Quantenfilm in einer Halbleiter-Heterostruktur

Heterostrukturen 3: Zulässige Energieniveaus (mit angedeuteter Wellenfunktion senkrecht zur Schicht im Grundzustand) der Bewegung senkrecht zur Schicht in einem Quantenfilm. Der hier unterstellte kastenförmige Potentialverlauf entspricht den Verhältnissen in einer sogenannten Doppelheterostruktur, bei der der Quantenfilm zwischen zwei Barrieren mit höherer Bandlücke eingegrenzt ist.

Heterostrukturen 4: Schichtaufbau eines Oberflächenemittierenden Halbleiterlasers. Die Spiegel des Resonators sind als Bragg-Spiegel wirkende Halbleiterübergitter.
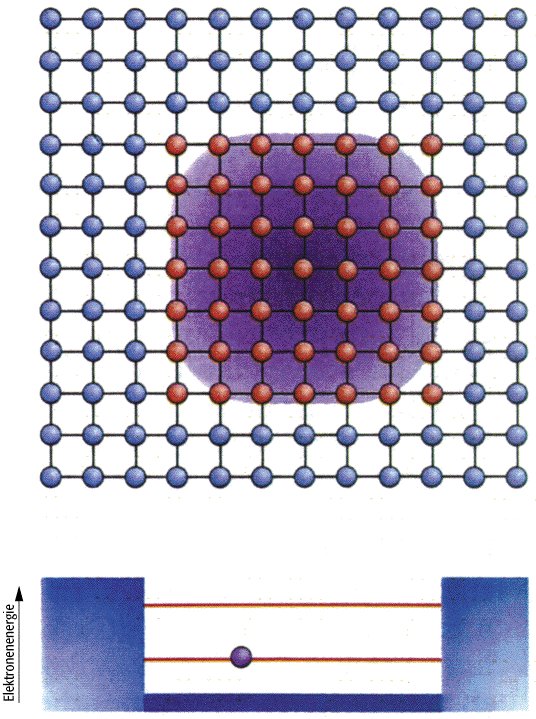
Heterostrukturen 5: Ein Quantenpunkt stellt die Realisierung eines dreidimensionalen Potentialtopfs für Ladungsträger dar. Diesen stehen deshalb nur einzelne, diskrete Energieniveaus zur Verfügung.

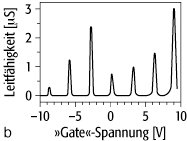
Heterostrukturen 6: Durch ›Gate‹-Elektroden definierter Quantenpunkt (a) und Leitfähigkeitsverhalten (b) in Abhängigkeit der Steuerspannung. Die breiten Leitfähigkeitsminima sind eine Folge der Coulomb-Blockade.

Heterostrukturen 7: Beim Aufwachsen eines Quantenfilms auf eine trapezförmig vorstrukturierte Schwelle kommt es durch die unterschiedlichenWachstumsgeschwindigkeit des Kristalls ›oben‹ und an den ›Hängen‹ des Trapezes zur Ausbildung eines Quantendrahts ohne ätzbedingte Randeffekte und mit kleinerer Breite als die ursprüngliche Trapezstruktur.

Heterostrukturen 8: Kraftmikroskopische Aufnahme von selbstordnenden Quantenpunkten aus Ge auf einem Si-Substrat.







Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.