Lexikon der Physik: Spindichtewellen
Spindichtewellen
Martin Dressel, Stuttgart
1 Definition
Die Spindichtewelle (spin density wave, SDW) ist ein antiferromagnetischer Grundzustand von Metallen, in welchem die Dichte der Leitungselektronenspins räumlich moduliert ist. In gewöhnlichen Antiferromagneten wie MnF2 sitzen einzelne magnetische Momente entgegengesetzter Orientierung stationär auf zwei kristallographischen Untergittern. Die SDW hingegen ist ein Vielteilchenphänomen mit einem itineranten Magnetismus, der nicht fest an das Kristallgitter gekoppelt ist.
SDW werden in Metallen und Legierungen beobachtet, häufig mit Übergangsmetallen; am bekanntesten sind Chrom und seine Verbindungen. Die SDW tritt auch als Grundzustand stark anisotroper Systeme auf wie eindimensionalen organischen Leitern.
Analog zur magnetischen Ordnung bei Antiferromagneten unterhalb der Néel-Temperatur wird das Elektronengas für Temperaturen kleiner einer Ordnungstemperatur 
instabil und geht in den kollektiven Ordnungszustand des itineranten Antiferromagneten über (Phasenübergang zweiter Ordnung, Phasenübergänge und kritische Phänomene); dies ist ein Zustand gebrochener Translationssymmetrie. Die Ursache der Instabilität des Elektronengases beim Übergang in den SDW-Grundzustand ist das sogenannte nesting der Fermi-Fläche.
2 Theorie
In einem Metall ist die Dichte der Leitungselektronen mit Spinrichtung 
und mit Spinrichtung 
überall identisch; die räumliche Variation der gesamten Ladungsdichte 
spiegelt die Periodizität des Kristallgitters wider. Bei Ausbildung einer SDW ist diese Translationsinvarianz nicht mehr gegeben: die Ladungsdichte 
hat nun eine sinusförmige Modulation
wobei 
die Amplitude und 
der Wellenvektor der SDW ist (siehe Abb. 1 ). Die Wellenlänge 
der SDW ist durch die Fermi-Fläche der Leitungselektronen gegeben und im allgemeinen nicht ein Vielfaches (d.h. kommensurabel mit) der Gitterperiode 
; das Verhältnis 
kann sich mit der Temperatur, dem äußeren Druck, der Dotierung oder anderen Parametern ändern. Die Spindichte 
ist die Differenz zwischen 
und 
:
Die Polarisation kann parallel zur Ausbreitungsrichtung 
liegen (longitudinale SDW) oder senkrecht zu ihr (transversale SDW). Zudem sind zirkulare Strukturen möglich, d.h. eine SDW mit helixförmiger Änderung der Magnetisierungsrichtung (siehe Abb. 2 ).
In der Hartree-Fock-Näherung wird der paramagnetische Grundzustand eines homogenen Elektronengases instabil, und es bildet sich eine SDW aus. Diese allgemeine Instabilität wird zwar durch die Abschirmung der Austauschwechselwirkung (Austausch) und der Coulomb-Barriere unterdrückt. Auf Grund einer besonders geformten Bandstruktur kann in einigen Metallen allerdings der SDW-Zustand doch auftreten. In gewissem Sinne kann man die SDW als eine Eigenschaft einer speziellen Topologie der Fermi-Fläche bezeichnen.
Für das Verständnis der SDW ist das nesting der Fermi-Fläche von grundsätzlicher Bedeutung. Hierunter versteht man die Eigenschaft, im reziproken (Impuls-) Raum Bereiche der Fermi-Fläche mit Elektron- und Lochcharakter durch einen Wellenvektor 
ineinander überführen zu können. Am offensichtlichsten ist der Fall in einer Dimension mit einer Fermi-Fläche aus zwei parallelen Ebenen bei 
(siehe Abb. 3 ). In zwei oder drei Dimensionen ist ein vollständiges nesting durch einen einzigen 
-Vektor nicht mehr möglich, doch kann es verschiedene Teile der Fermi-Fläche geben, die durch Translation um unterschiedliche 
mehr oder weniger gut ineinander überführt werden; im Fall von Cr beispielsweise würfelförmige Gebilde (siehe Abb. 4 ).
Die Austauschwechselwirkung zwischen zwei Elektronen mit parallelem Spin reduziert die Coulomb-Wechselwirkung auf Grund des Pauli-Prinzips. Dies führt zu einem Energiegewinn bei der Ausbildung einer SDW, die ja eine Modulation der Dichte der Elektronenspins gemäß Gl. (2) bedeutet. Aufgewendet werden muß hierfür allerdings kinetische Energie. Im Bild von Energiebändern öffnet sich eine Energielücke
an der Fermi-Kante (siehe Abb. 5 ), die mit abnehmender Temperatur in der gleichen Weise wie die Magnetisierung (siehe Abb. 6 ) zunimmt. Der elektrische Widerstand unterhalb 
zeigt deshalb halbleitende Eigenschaften. Im Gegensatz zu den lokalen Spins eines Antiferromagneten ist die SDW nicht fest mit dem Gitter verbunden, sondern frei; sie hängt höchstens an Fehlstellen im Kristall. Neben dem Einteilchentransport kann die SDW deshalb auch als Ganzes bewegt werden, wenn ein gewisses elektrisches Schwellfeld überschritten wird, um die Dichtewellen von Haftzentren loszureißen, oder ein elektrisches Wechselfeld der passenden Frequenz 
angelegt wird. Dies ist ein kollektiver Ladungstransport ähnlich der Supraleitung (siehe Abb. 10 ).
Es besteht eine gewisse Analogie von SDW und Ladungsdichtewelle (charge density wave, CDW, Ladungsdichtewellensysteme), die ebenfalls eine Instabilität des Elektronengases ist. Wie bei der SDW öffnet sich eine Energielücke an der Fermi-Kante, und der geordnete Zustand ist halbleitend. Allerdings bedeutet die CDW eine Modulation der gesamten Dichte 
der Leitungselektronen, die einher geht mit einer nicht unbedingt kommensurablen Überstruktur des Kristallgitters.
3 Experimenteller Nachweis
Da sich in der SDW-Phase nur eine magnetische Überstruktur in den Leitungselektronen ausbildet, die elektronische Gesamtdichte 
jedoch unverändert bleibt, ist ein Nachweis mittels Röntgenstreuung, wie bei CDW-Systemen, nicht möglich. Spin-polarisierte Neutronenstreuung erlaubt allerdings den eindeutigen Nachweis des magnetischen Ursprungs der SDW. Aus den Bragg-Reflexen der elastischen Neutronenstreuung kann der Wellenvektor 
der Magnetisierungswellen und die Stärke des magnetischen Moments 
bestimmt werden. Bei fluktuierenden Feldern ist inelastische Neutronenstreuung möglich; aus dem dynamischen Strukturfaktor kann die Magnetisierung ermittelt werden. Die Temperaturabhängigkeit der Magnetisierung (d.h. des internen magnetischen Feldes) wird durch die Brillouin-Funktion und die mean-field-Theorie beschrieben (siehe Abb. 6 und Abb. 8 ).
Die magnetische Suszeptibilität zeigt die für einen Antiferromagneten typische Anisotropie. Der Anteil der SDW zur Suszeptibilität verschwindet entlang der leichten Magnetisierungsrichtung 
, der Komponente des Suszeptibiliätstensors parallel zur Polarisationsrichtung der SDW; senkrecht dazu ist 
nur sehr schwach temperaturabhängig (siehe Abb. 7 ). Einen eindeutigen Hinweis auf die magnetische Ordnung im SDW-Zustand geben antiferromagnetische Resonanzen, deren Frequenz-, Temperatur- und Winkelabhängigkeiten mittels Elektronenspinresonanz untersucht werden können. Durch Kernspinresonanz- oder Mößbauer-Untersuchungen (Mößbauer-Effekt) an den Atomen des Kristallgitters kann das interne Magnetfeld der SDW bestimmt werden.
Als kollektiver Ordnungszustand der Leitungselektronen öffnet sich beim Übergang in den SDW-Grundzustand eine Energielücke an der Fermi-Kante. Abhängig davon, ob sie sich über die ganze Brillouin-Zone erstreckt oder das Metall nur Teile der Fermi-Fläche verliert, führt dies zu einer mehr oder weniger starken Änderung der thermodynamischen Größen wie der spezifische Wärme oder thermischen Ausdehnung. Das Öffnen der Energielücke 
führt auch zu einem Anstieg des elektrischen Widerstands 
auf Grund der reduzierten Ladungsträgerdichte beim Unterschreiten der Ordnungstemperatur 
. Erstreckt sich das nesting über die gesamte Fermi-Fläche wie in den eindimensionalen Systemen, so ist die SDW-Phase isolierend (siehe Abb. 9 ). Wenn nur ausgewählte 
-Vektoren die nesting-Bedingung erfüllen, ist der Transport anisotrop, und man beobachtet lediglich ein lokales Maximum in 
unter 
.
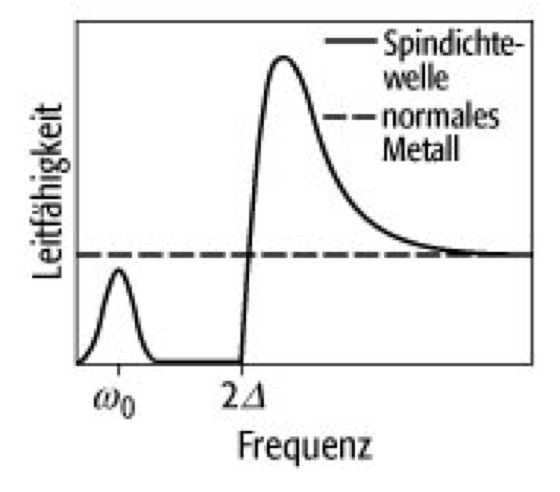
Optische Untersuchungen erlauben die Energielücke direkt zu bestimmen, da bei 
die optische Leitfähigkeit stark reduziert ist (siehe Abb. 10 ). Die Resonanz bei 
entspricht der kollektiven Anregung der SDW. Diese kann auch als Ganzes zum Ladungstransport beitragen, wenn ein angelegtes Gleichfeld eine Schwelle der Haftung an Störstellen überschreitet.
4 Beispiele
Chrom ist das einzige reine Metall, das itineranten Antiferromagnetismus zeigt. Ähnlich wie bei α-Mn und γ-Fe sind hierfür die 3d-Elektronen verantwortlich, im Gegensatz zu den Lanthaniden und Actinoiden, die den Magnetismus der lokalisierten f-Elektronen zeigen. Oberhalb des antiferromagnetischen Übergangs bei TSDW = 311 K existieren in Cr keine lokalisierten magnetischen Momente. Der Wellenvektor der antiferromagnetischen Struktur liegt entlang der (100)-Richtung, ist jedoch inkommensurabel mit dem Kristallgitter (siehe Abb. 4 ). Die transversale Modulation der magnetischen Momente 
, welche ca. 2,8 μB stark sind, geht bei 120 K durch spin-flip in eine longitudinale Modulation über (siehe Abb. 6 ).
Unter den niedrigdimensionalen Metallen dient (TMTSF)2PF6 (TMTSF = Tetramethyltetraselenafulvalen) als Modellsystem für eine eindimensionale SDW. Im dem Kristall sind die flachen TMTSF-Moleküle in a-Richtung übereinander gestapelt; entlang der Stapel, die durch die Anionen wie PF 
in c-Richtung von einander getrennt sind, ist die elektrische Leitfähigkeit 3000mal größer als senkrecht dazu (siehe Abb. 9 ). Auf Grund der schwachen Kopplung in b-Richtung zwischen den TMTSF-Ketten sind die Fermi-Flächen keine Ebenen, sondern leicht gewellt (siehe Abb. 3 ). Die SDW ist mit μ0 = 0,08 μB sehr schwach; sie ist transversal parallel zu b polarisiert und nicht kommensurabel mit dem Gitter.
Literatur:
[1] A.W. Overhauser, Spin Density Waves in an Electron Gas, Physical Review 128, 1437-1452, 1962.
[2] N.I. Kulikov und V.V. Tugushev, Spin-density wave and itinerant antiferromagnetism in metals, Soviet Physics Uspekhi 27, 954-976, 1984.
[3] E. Fawcett, Spin-density-wave antiferromagnetism in chromium, Review of Modern Physics 60, 210-283, 1988.
[4] G. Grüner, Density Waves in Solids, Addison-Wesley, Reading, 1994.
![](javascript:ShowPic("/lexika/images/physik/fff13505.jpg", "328", "358");)
Spindichtewellen 1: Vergleich der gesamten und partiellen Ladungsdichten 
, 
, 
und der Spindichte 
eines Metalls im normalen und SDW-Zustand.
![](javascript:ShowPic("/lexika/images/physik/fff13518.jpg", "327", "433");)
Spindichtewellen 2: Unterschiedliche Typen von Spindichtewellen: a) transversale SDW, b) longitudinale SDW, c) chirale SDW, d) geneigte SDW und e) ferromagnetische SDW.
![](javascript:ShowPic("/lexika/images/physik/fff13521.jpg", "327", "315");)
Spindichtewellen 3: In einem streng eindimensionalen System besteht die Fermi-Fläche aus zwei parallelen Ebenen (gestrichelte Linien), und der nesting-Vektor ist 
. Durch Abweichungen von der Eindimensionalität sind die Flächen leicht gewellt, doch ist ein nesting weiterhin möglich.
![](javascript:ShowPic("/lexika/images/physik/fff13525.jpg", "189", "189");)
Spindichtewellen 4: Schnitt durch die schematische Fermi-Fläche von Cr. Die schraffierten Bereiche zeigen die Lochbänder. Es sind zwei typische nesting-Vektoren eingezeichnet.
![](javascript:ShowPic("/lexika/images/physik/fff13527.jpg", "188", "181");)
Spindichtewellen 5: Die im Impulsraum verschobenen Energieniveaus für Elektronen mit Spin 
und 
führen zu einer Energieaufspaltung von 
; nur der untere Teil ist besetzt.
![](javascript:ShowPic("/lexika/images/physik/fff13531.jpg", "330", "271");)
Spindichtewellen 6: Die Temperaturabhängigkeit der magnetischen Bragg-Reflexe aus Neutronenstreuung an Chrom. Unterhalb TSDW = 311 K bildet sich die SDW; bei TSF = 120 K ordnen sich die Spins um.
![](javascript:ShowPic("/lexika/images/physik/fff13544.jpg", "191", "148");)
Spindichtewellen 7: Die Temperaturabhängigkeit der magnetischen Suszeptibilität von (TMTSF)2PF6. Die leichte Magnetisierungsachse ist entlang der b-Richtung, die harte entlang c.
![](javascript:ShowPic("/lexika/images/physik/fff13541.jpg", "191", "146");)
Spindichtewellen 8: Die Temperaturabhängigkeit der Stärke der SDW in (TMTSF)2PF6. Die experimentellen Daten wurden mit unterschiedlichen Meßmethoden ermittelt.
![](javascript:ShowPic("/lexika/images/physik/fff13548.jpg", "191", "314");)
Spindichtewellen 9: Die Temperaturabhängigkeit des spezifischen Widerstands in (TMTSF)2PF6 senkrecht und parallel zu den Stapeln. Der Übergang zur halbleitenden SDW-Phase ist bei TSDW = 12 K zu erkennen.
![](javascript:ShowPic("/lexika/images/physik/fff13534.jpg", "191", "168");)
Spindichtewellen 10: Die Frequenzabhängigkeit der optischen Leitfähigkeit eines Metalls in normalem und SDW-Zustand. Ab der Frequenz 
sind Anregungen über die SDW-Energielücke möglich. Bei 
beobachtet man eine resonanzartige Mode auf Grund der Haftung der SDW.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.