24 Kreise im Quadrat
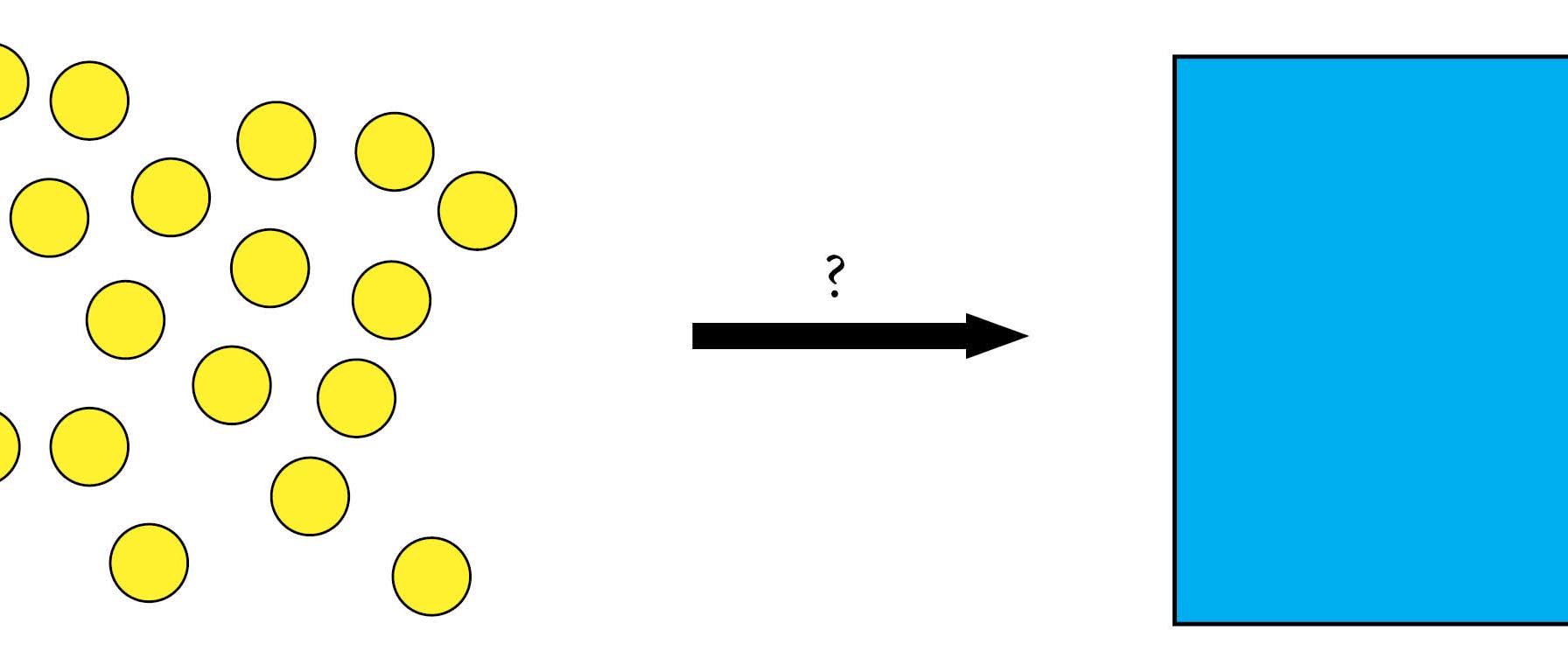
Legen Sie 24 gleiche Kreise nebeneinander in ein möglichst kleines Quadrat.
Diese Fragestellung zählt zu den Problemen der dichtesten Kugelpackungen. Für nicht zu große Quadratzahlen (auch noch für 25) ist die entsprechende Lösung ganz einfach eine Anordnung im quadratischen Raster. Nehmen Sie einen Kreis etwa aus der Mitte heraus und lassen Sie den Rest näher zusammenrücken (beziehungsweise entsprechend größer werden).
Von mehreren Möglichkeiten ist dies die mit der höchsten Symmetrie:
Verbindet man die Mittelpunkte benachbarter Kreise, so kann man die Länge der Diagonale des Quadrats mit üblichen Mitteln (Diagonale im Quadrat, Höhe im gleichseitigen Dreieck) leicht ermitteln. Sie beträgt \(2 + 6 \sqrt2+2\sqrt3\), wobei der Kreisradius gleich 1 gesetzt wird. Damit beträgt die Seitenlänge des Quadrats \(\sqrt2+6+\sqrt6 \approx 9{,}8637\) Kreisradien. Dank an Roland Schröder für den Hinweis.
Schreiben Sie uns!
Beitrag schreiben