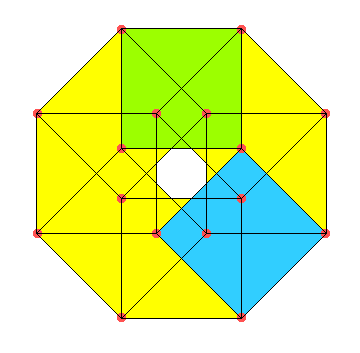
Acht Quadrate

Acht Quadrate haben zusammen bekanntlich 32 Ecken. Kann man auch mit halb so vielen auskommen, wenn einige mehrfach benutzt werden? Dabei müssen die Quadrate zwar alle gleich groß sein, dürfen sich jedoch teilweise (aber nie ganz) überlappen. Aber eine ganze Seite gemeinsam haben dürfen sie nicht, sonst wär's zu einfach: Ein 2x4-Ausschnitt aus einem Schachbrett käme sogar mit 15 Ecken aus.
Die Ecken liegen auf zwei regelmäßigen Achtecken.
Im Kreuzgang des Paderborner Doms gibt es das berühmte Hasenfenster:

Ein Kinderscherz geht so: Die Kuh hat 8 Beine, 2 vorne, 2 hinten, 2 rechts und 2 links.
Aber was hat das Ganze mit der 4. Dimension zu tun?
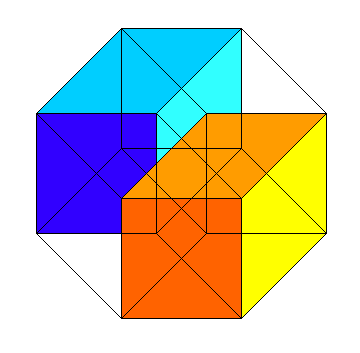
Das Maßpolytop der 4. Dimension (Hyperwürfel, Tesserakt, Oktochor) hat 16 Ecken, 32 Kanten, 24 Quadrate und 8 Würfel. Unser Bild kann als Parallelprojektion eines Hyperwürfels in die 2. Dimension aufgefasst werden. Dabei sind alle Kanten unverkürzt zu sehen, 8 Quadrate unverzerrt und 16 zu Rhomben verzerrt. Zwei der Würfel sind hier farblich hervorgehoben:



Schreiben Sie uns!
Beitrag schreiben