Algebraisierung


Verwandeln Sie bitte die getönte Fläche durch Zerschneiden in 7 Teile in ein Rechteck und bestimmen Sie daraus den Flächeninhalt.
Einige Schnittlinien sind Radien.
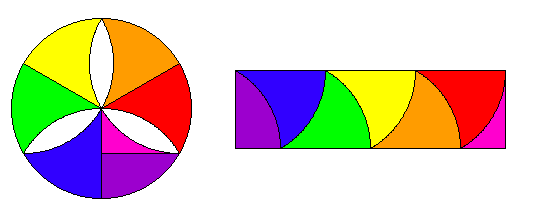
Die Fläche ist also \(3 r^2\cdot\sqrt{3/4}\). Darin kommt erstaunlicherweise \(\pi\) nicht vor. Bekanntlich ist \(\pi\) keine algebraische, sondern eine transzendente Zahl, d. h. sie kann insbesondere nicht als Wurzel aus ganzen Zahlen ausgedrückt werden. Unsere Fläche ist als Funktion des Radius \(r\) zwar nicht rational, aber immerhin algebraisch.
Das Ganze ist nicht mehr ganz so erstaunlich, wenn man sich überlegt, wie man die Fläche in ein regelmäßiges Sechseck umbauen kann:
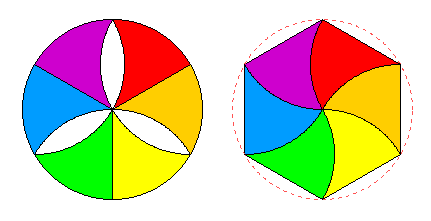
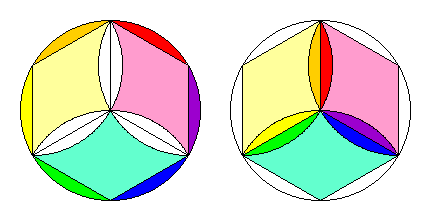
Man kann sich darüber streiten, welche Lösung die einfachere ist, auch formal: Die obere hat nur 6 Teile, aber die Hälfte von ihnen muss man umklappen.



Schreiben Sie uns!
Beitrag schreiben