Hemmes mathematische Rätsel: Auf wie viele Arten kann man die Felder mit 31 Dominos bedecken?
Der Philosoph Max Black (1909–1988) veröffentliche wichtige Arbeiten zur Philosophie der Sprache, zur Philosophie der Mathematik und der Naturwissenschaften und der Kunst. In seinem 1946 veröffentlichten Buch »Critical Thinking« findet man eine ganze Reihe kniffliger mathematischer Denksportaufgaben. Dort erscheint erstmals das inzwischen bekannte Problem des zerstörten Schachbretts.
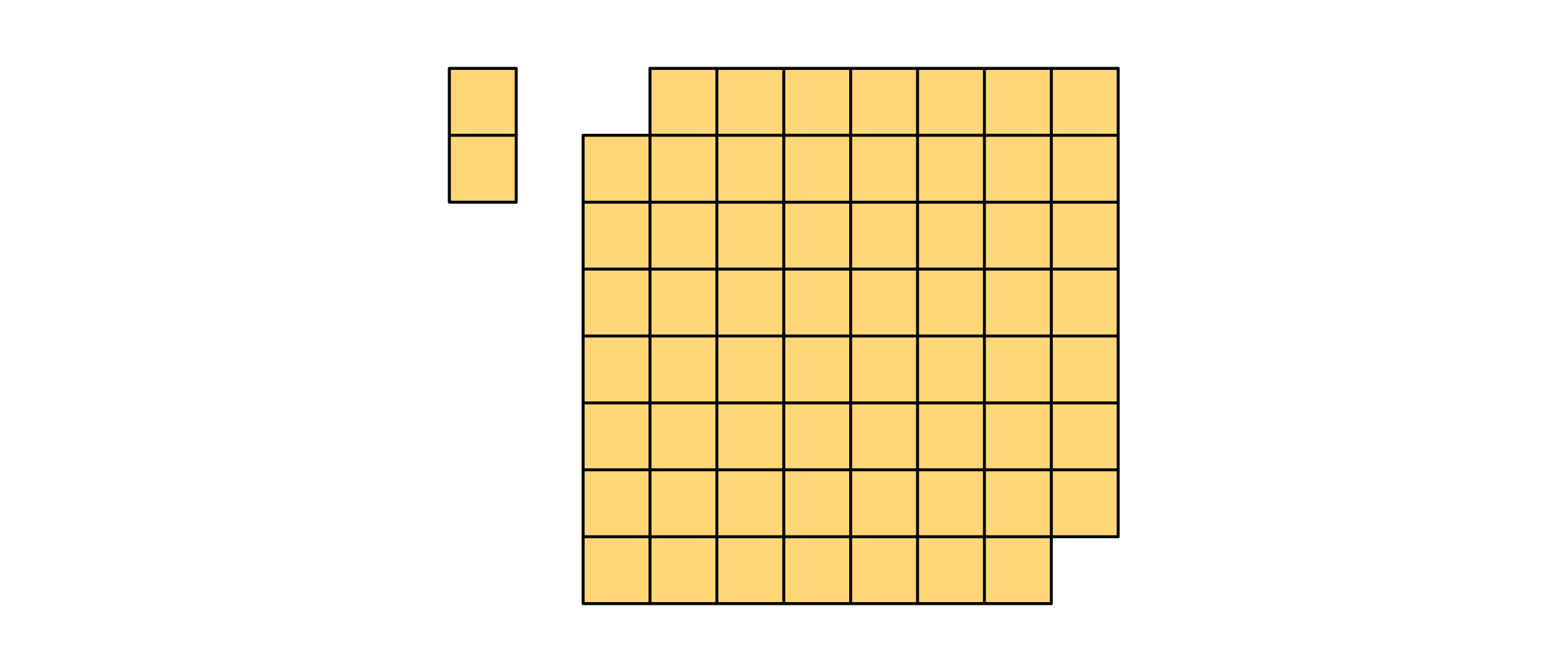
Bei einem Schachbrett sind zwei sich diagonal gegenüberliegende Eckfelder herausgesägt worden. Wie viele verschiedene Möglichkeiten gibt es, mit 31 Dominosteinen, die jeweils die Größe von genau zwei Schachfeldern haben, die übrig gebliebenen 62 Felder vollständig zu bedecken?
Ein Schachbrett hat 32 weiße und 32 schwarze Felder, und sich diagonal gegenüberliegende Eckfelder sind gleichfarbig. Sägt man sie heraus, so bleiben 32 Felder von der einen und 30 von der anderen Farbe übrig. Ein Dominostein deckt immer ein weißes und ein schwarzes Feld ab, 31 Steine bedecken also 31 schwarze und 31 weiße Felder. Da es aber von der einen Farbe nur 30 Felder gibt, ist eine solche Bedeckung des Schachbretts unmöglich.
Schreiben Sie uns!
Beitrag schreiben