Hemmes mathematische Rätsel: Das Pentagramm
1970 gründeten die beiden bekannten russischen Wissenschaftler A. N. Kolmogorov und I. K. Kikoyin die Zeitschrift »Kvant«, in der von Fachautoren auf anschauliche Weise über aktuelle Themen der Mathematik und der Physik für ein breites Publikum geschrieben wird. Die Zeitschrift wurde ein so großer Erfolg, dass ab 1990 auch eine amerikanische Ausgabe mit dem Titel »Quantum« erschien, die neben Übersetzungen aus der russischen Ausgabe auch Originalartikel publizierte. Leider blieb der amerikanischen Ausgabe der Erfolg der russischen versagt, so dass sie nach elf Jahren wieder eingestellt wurde. Das heutige Rätsel stammt aus dieser Zeitschrift.
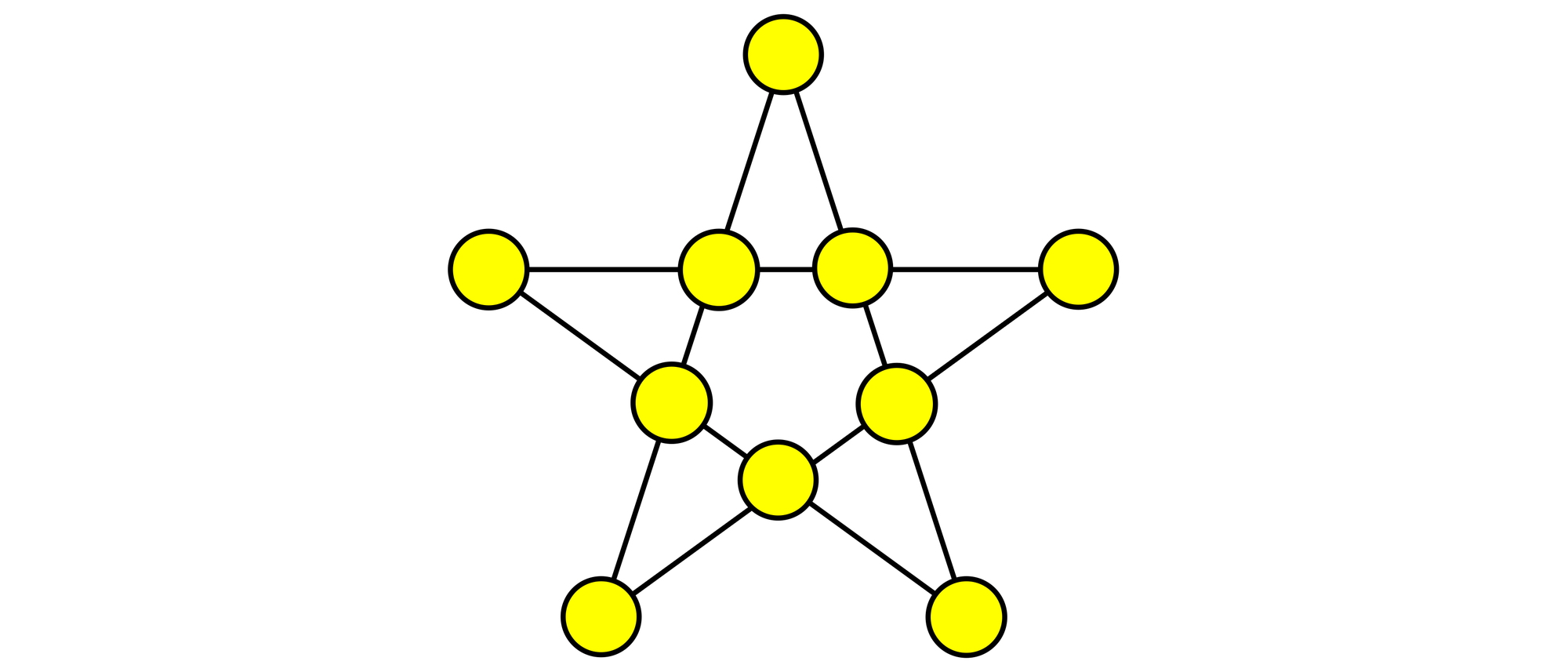
Versuchen Sie, in die zehn runden Felder des Pentagramms verschiedene positive ganze Zahlen zu setzen, so dass in allen fünf Reihen die Summe der vier Felder jeweils eine ungerade Zahl ergibt. Die Summe aller zehn Zahlen soll außerdem so klein wie möglich sein.
Angenommen, die Aufgabe sei lösbar, dann würde in jeder der fünf Reihen die Summe der vier Felder ungerade sein. Zählt man diese fünf Reihensummen zusammen, erhält man auch wieder eine ungerade Zahl N, denn die Summe von fünf ungeraden Zahlen ist immer ungerade. Da jedes Feld des Pentagramms zu zwei Reihen gehört, ist N das Doppelte der Summe M der Zahlen auf den Feldern. Weil aber N = 2M eine gerade Zahl ist, gibt es keine Lösung für das Problem.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.