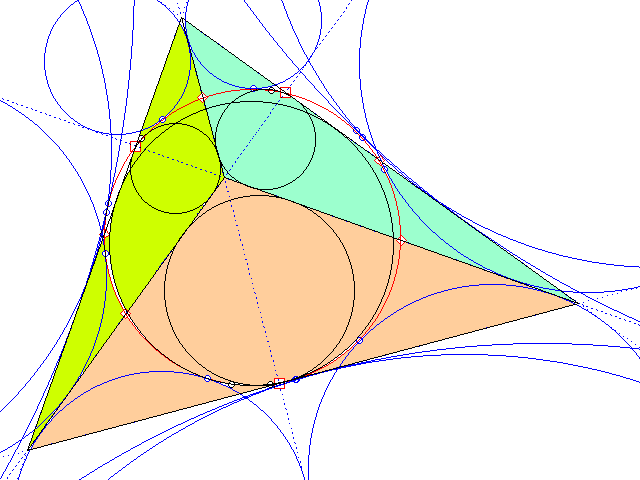
1821 hat Jean-Victor Poncelet (1788–1867) dargelegt, dass jedes Deieck einen Neunpunktekreis hat. Dieser geht durch die 3 Höhenfußpunkte, die 3 Seitenmitten und die 3 Ecken des vom Höhenschnittpunkt aus "halbierten" (d. h. zentrisch im Maßstab 1/2 gestreckten) Dreiecks. Sein Mittelpunkt ist die Mitte von Höhenschnittpunkt und Umkreismitte.

Karl Wilhelm Feuerbach (1800–1834) hat diesen Kreis noch einmal in seinem 1822 in Nürnberg erschienenen Buch "Eigenschaften einiger merkwürdigen Punkte des geradlinigen Dreiecks, und mehrerer durch sie bestimmten Linien und Figuren" beschrieben, aber darin noch besonders den später nach ihm benannten (und nicht leicht zu beweisenden) Satz festgestellt:

Der Neunpunktekreis berührt den Inkreis des Dreiecks.

Später hat man gefunden, dass er auch die drei Ankreise berührt.

Damit sind wir schon bei 13 Punkten auf dem Kreis. Es kommt aber noch besser: Wenn H der Höhenschnittpunkt eines Dreiecks ABC ist, so ist auch C der Höhenschnittpunkt von ABH, B der von AHC und A der von HBC.

Alle vier Dreiecke haben (zusammen!) nur 3 Höhenfußpunkte, denn die 6 Geraden AB, AC, BC, AH, BH und CH schneiden sich zu 3 Paaren rechtwinklig: AB und CH, BC und AH, AC und BH. Wenn aber alle 4 Dreiecke nur 3 gemeinsame Höhenfußpunkte haben, haben sie auch nur einen gemeinsamen Neunpunktekreis. Dieser berührt also auch die An- und Inkreise aller genannten Dreiecke.

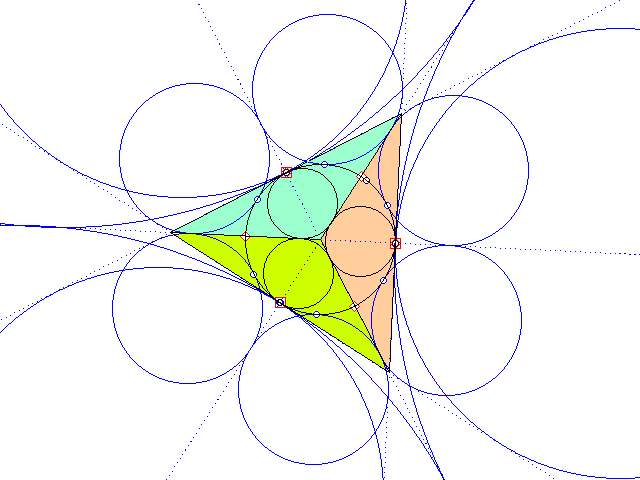
Im Allgemeinen fallen diese 16 Berührpunkte nicht zu mehreren zusammen, wohl aber im gleichseitigen Dreieck und seinen drei Teilen, wobei sich 24 Punkte auf 12 Punkte verteilen und der Berührpunkt des Inkreises des gleichseitigen mit dem Neunpunktekreis nicht als Punkt existiert, da dann diese beiden Kreise voll zusammenfallen (das Bild zeigt ungenauerweise trotzdem einen überzähligen Punkt).