Hemmes mathematische Rätsel: Der Arbelos
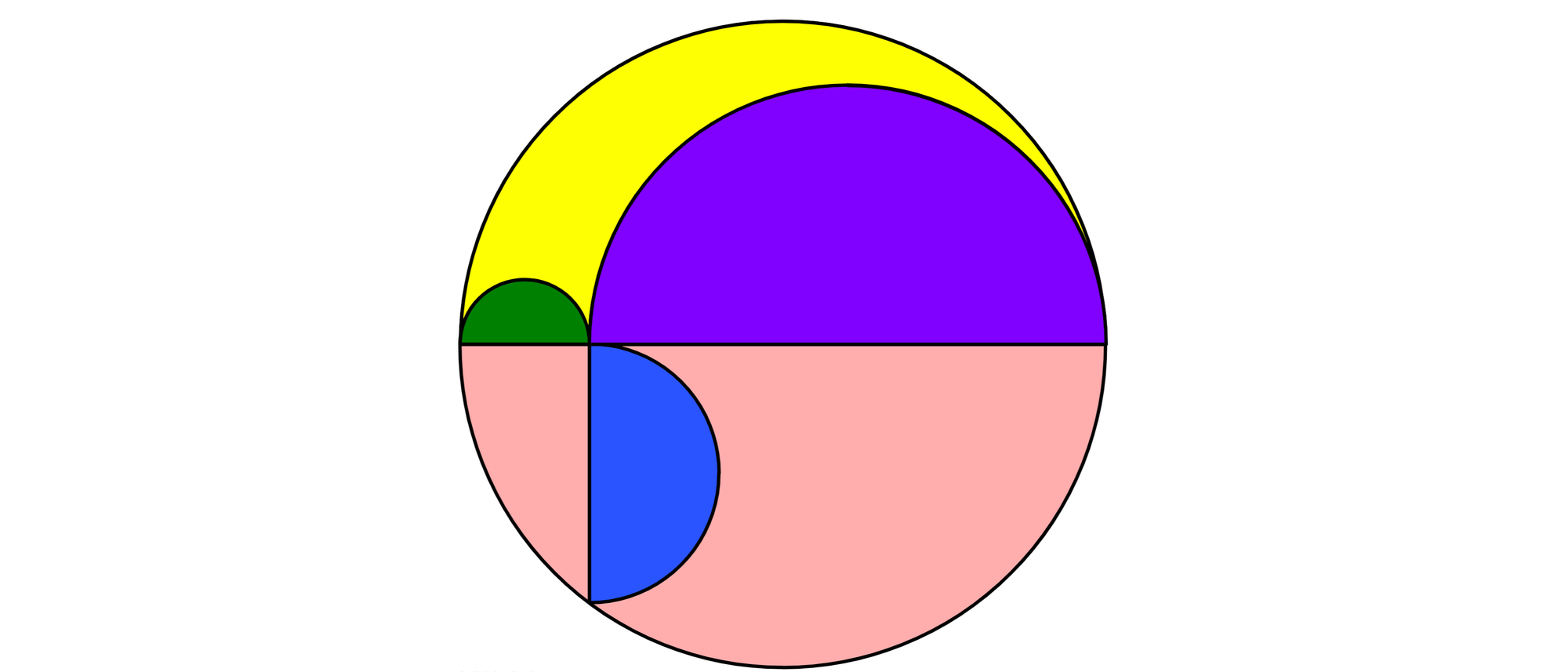
Der griechische Wissenschaftler Archimedes, der um 287 vor Christus geboren wurde und 212 vor Christus starb, lebte auf Sizilien und gilt als der bedeutendste Mathematiker, Physiker und Ingenieur der Antike. In seinem »Buch der Lemmata«, das allerdings nicht mit letzter Sicherheit tatsächlich von ihm stammt, wird eine Figur analysiert, die von drei Halbkreisen begrenzt und »Arbelos« genannt wird. Sie verdankt ihren Namen dem Schustermesser, das auf Griechisch Arbelos heißt und eine Klinge besitzt, die ganz ähnlich geformt ist. Die gelbe Figur in der Zeichnung ist ein Arbelos.
Der grüne und der lila Halbkreis liegen auf dem Durchmesser des Außenkreises. Der Durchmesser des grünen Halbkreises steht zum Durchmesser des lila Halbkreises im Verhältnis \(x\). In welchem Verhältnis, in Abhängigkeit von \(x,\) steht der Inhalt des Arbelos zum Inhalt des blauen Halbkreises?
Verbindet man die Enden des Durchmessers des Außenkreises mit der Ecke des blauen Halbkreises, mit der dieser den Außenkreis berührt, entsteht ein Dreieck (rot), das nach dem Satz des Thales rechtwinklig ist. Dessen Hypotenusenhöhe ist der Durchmesser des blauen Halbkreises. Nach dem Höhensatz des Euklid ist das Produkt der beiden Hypotenusenabschnitte gleich dem Höhenquadrat.Bezeichnet man die Radien der drei Halbkreise mit \(a, b\) und \(c,\) so gilt deshalb \((2a)\cdot (2b)=(2c)^2\) oder \(ab = c^2.\)
Um die Fläche \(A\) des Arbelos zu bestimmen, muss man von der halben Fläche des Außenkreises die Flächen des grünen und des lila Halbkreise abziehen. Es gilt also \(A=\frac{1}{2}\pi(a+b)^2 -\frac{1}{2}\pi a^2 -\frac{1}{2}\pi b^2,\) was sich zu \(A=\pi ab\) vereinfachen lässt.
Der blaue Halbkreis hat den Inhalt \(B =\frac{1}{2}\pi c^2.\) Da \(c^2=ab\) ist, wird daraus \(B=\frac{1}{2}\pi a b.\)
Damit bekommt man für das gesuchte Verhältnis \(\frac{A}{B}=\frac{\pi a b }{\frac{1}{2}\pi a b}=2.\) Dieser Wert ist unabhängig von Durchmesserverhältnis \(x\) des grünen und des lila Halbkreises.
Schreiben Sie uns!
Beitrag schreiben