Hemmes mathematische Rätsel: Der dritte Kreis
Bernd Hülsmann aus Jülich in Nordrhein-Westfalen erdachte sich 2015 ein geometrisches Rätsel, das er in den beiden Aachener Tageszeitungen veröffentlichte.
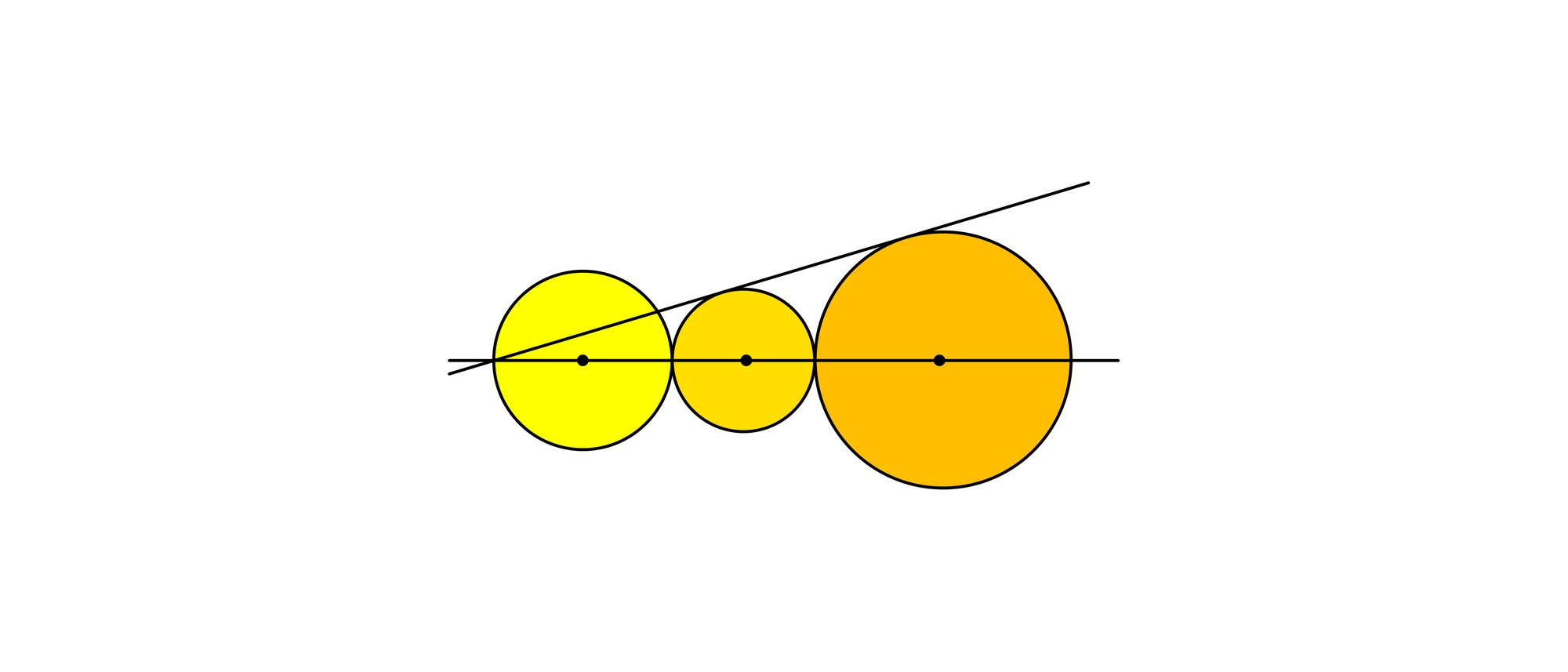
Drei Kreise, deren Mittelpunkte auf einer Geraden liegen, stoßen mit ihren Umfängen aneinander. Der erste Kreis hat den Radius 10 und der zweite 8. Durch den äußeren Schnittpunkt des ersten Kreises mit der Geraden läuft eine zweite Gerade, die den zweiten und auch den dritten Kreis tangiert. Wie groß ist der Radius des dritten Kreises?
In jedem Punkt eines Kreisumfangs stehen der Radius und die Tangente senkrecht zueinander. Folglich liegen der Radius des zweiten und der des dritten Kreises zu den Berührungspunkten der gemeinsamen Tangente parallel zueinander. Somit gilt nach dem Strahlensatz r/(10+10+8+8+r) = 8/(10+10+8), was sich zu r/(36+r) = 8/28 zusammenfassen lässt. Löst man die Gleichung nach r auf, erhält man r = 72/5 = 14,4.
Hat Ihnen dieses Rätsel gefallen? Dann rätseln Sie doch einfach direkt weiter:
- Was ist die nächste Zahl in der Reihe?
- Wie groß ist x in diesen Dreiecken?
- Was ist die kleinste Zahl, die diesen Bedingungen gehorcht?
- Wie viele Dreiecke enthält diese Figur?
- Wie lang ist die Sehne des Kreises?
- Welche Zahl fehlt?
- Wie groß ist die Fläche des Halbkreises?
- Mit welcher Zahl muss die Reihe fortgesetzt werden?
- Wie viel deckt das Quadrat ab?
- Wie muss das Streichholz umgelegt werden?
- Wie viele Turmquadrate passen ins Schachbrett?
- Wie lang sind die Seiten des Quadrats?
Eine Übersicht über alle Matherätsel finden Sie unter https://www.spektrum.de/raetsel/. Viel Spaß beim Weiterknobeln!
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.