Der Präsident als Trapezkünstler?

Der spätere Präsident der USA James Abram Garfield (1831-1881, im Amt 1881) hat um 1876 den pythagoreischen Satz mit einem Trapez bewiesen. Wie?
Das Trapez besteht aus einem halbem Hypotenusenquadrat und zweimal dem rechtwinkligen Dreieck.
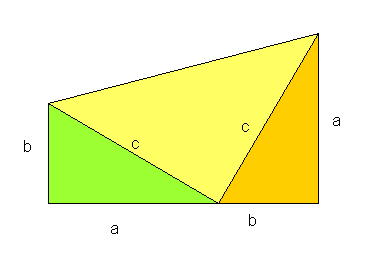
Die Fläche des Trapezes ist das Produkt aus Mittelparallele \((a + b)/2\) und Höhe \(a + b\), also \(a^2/2+b^2/2+ab\), andererseits haben die beiden kleinen Dreiecke zusammen die Fläche \(ab\), das große \(c^2/2\).
Loomis führt diesen Beweis von Garfield als 231. der "geometrischen" Beweise auf.
Nach meiner Meinung ist der Beweis dadurch, dass er nur die Hälfte einer besonders gut einleuchtenden Beweisfigur (welcher?) darstellt, nicht besonders einfach oder elegant. Man würde ihn vermutlich nicht so besonders hervorheben, wenn sein Erfinder nicht auch US-Präsident gewesen wäre. Für die heutige Jugend ist möglicherweise die Namensgleichheit zu einem Comic-Kater noch eher motivierend.



Schreiben Sie uns!
Beitrag schreiben