Hemmes mathematische Rätsel: Der unbekannte Winkel
1975 wurde in Kanada die Zeitschrift »Eureka« von der Carleton-Ottawa Mathematics Association ins Leben gerufen. Sie richtet sich an Abiturienten und Studienanfänger und publiziert in erster Linie mathematische Probleme und ihre Lösungen. Im Laufe der letzten vier Jahrzehnte ist sie zu einer der weltweit größten Sammlungen mathematischer Knobeleien angewachsen. 1978 wurde »Eureka« in »Crux Mathematicorum« umbenannt, um nicht mit einer gleichnamigen Zeitschrift der Cambridge University Mathematical Society verwechselt zu werden. 1985 übernahm die Canadian Mathematical Society die Herausgabe der Zeitschrift. Einer der vielen Autoren, die der Zeitschrift Aufgaben zusandten, war Mathematiker Andrejs Dunkels. Er wurde 1939 in der lettischen Stadt Riga geboren und floh 1944 mit seinen Eltern vor den Nazis nach Schweden. Er studierte in Uppsala Mathematik und Physik und wurde Lehrer und Dozent an der Universität Luleå. 1998 starb er nach er nach langer Krankheit.
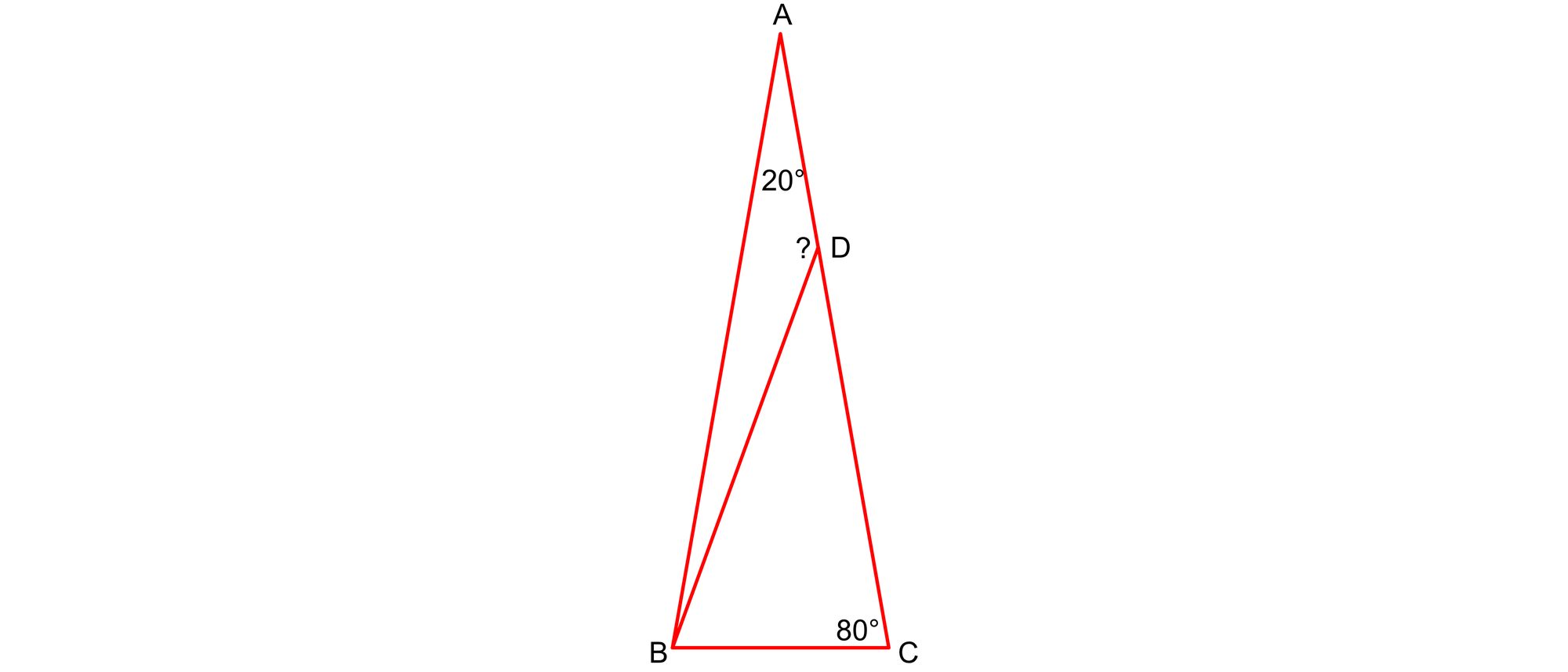
Im Oktober 1976 stellte er den Lesern von »Eureka« ein hübsches geometrisches Problem. In dem Dreieck ABC ist die Strecke AD genauso lang wie die Seite BC. Wie groß ist der mit einem Fragezeichen gekennzeichnete Winkel?
Zunächst einmal errichten wir außerhalb des Dreiecks ABC auf der Strecke AD ein gleichseitiges Dreieck ADE und verbinden die beiden Punkte B und E miteinander. Die vier Strecken AD, DE, EA und BC sind gleich lang. Da der Winkel CBA, genau wie der Winkel ACB, eine Größe von 80° hat, ist das Dreieck ABC gleichschenklig. Auch der Winkel BAE ist 80° groß, da der Winkel DAE (des gleichseitigen Dreiecks) 60° beträgt.
Bei dem Dreieck ABC sind die beiden Seiten BC und AC und der von ihnen eingeschlossene Winkel ACB genauso groß wie die entsprechenden Seiten EA und BA und der entsprechende Winkel BAE bei dem Dreieck BEA. Folglich sind die beiden Dreiecke ABC und BEA gleich. Somit sind auch die beiden Dreiecke ABD und BED deckungsgleich und die Winkel ADB und BDE gleich groß. Da die Summe der drei am Punkt D zusammentreffende Winkel 360° beträgt, muss der gesuchte Winkel ADB eine Größe von ½(360° − 60°) = 150° haben.



Schreiben Sie uns!
Beitrag schreiben