Hemmes mathematische Rätsel: Der Würfelstapel
Seit 1983 wird in den Schulen der USA jährlich ein Mathematikwettbewerb ausgetragen, der den Namen Mathcounts trägt. Mehr als 30 000 Schülerinnen und Schüler beteiligen sich jeweils an der ersten Runde, 5000 schaffen es in die zweite Runde und 228 nehmen schließlich an der Endrunde teil. 1999 gaben Patrick Vennebush und Terrel Trotter ein Buch mit dem Titel »The All-Time Greatest Mathcounts Problems« heraus, in dem sie die besten 150 Aufgaben dieses Wettbewerbs zusammengestellt hatten. Aus diesem Buch stammt das folgende kleine Geometrieproblem:
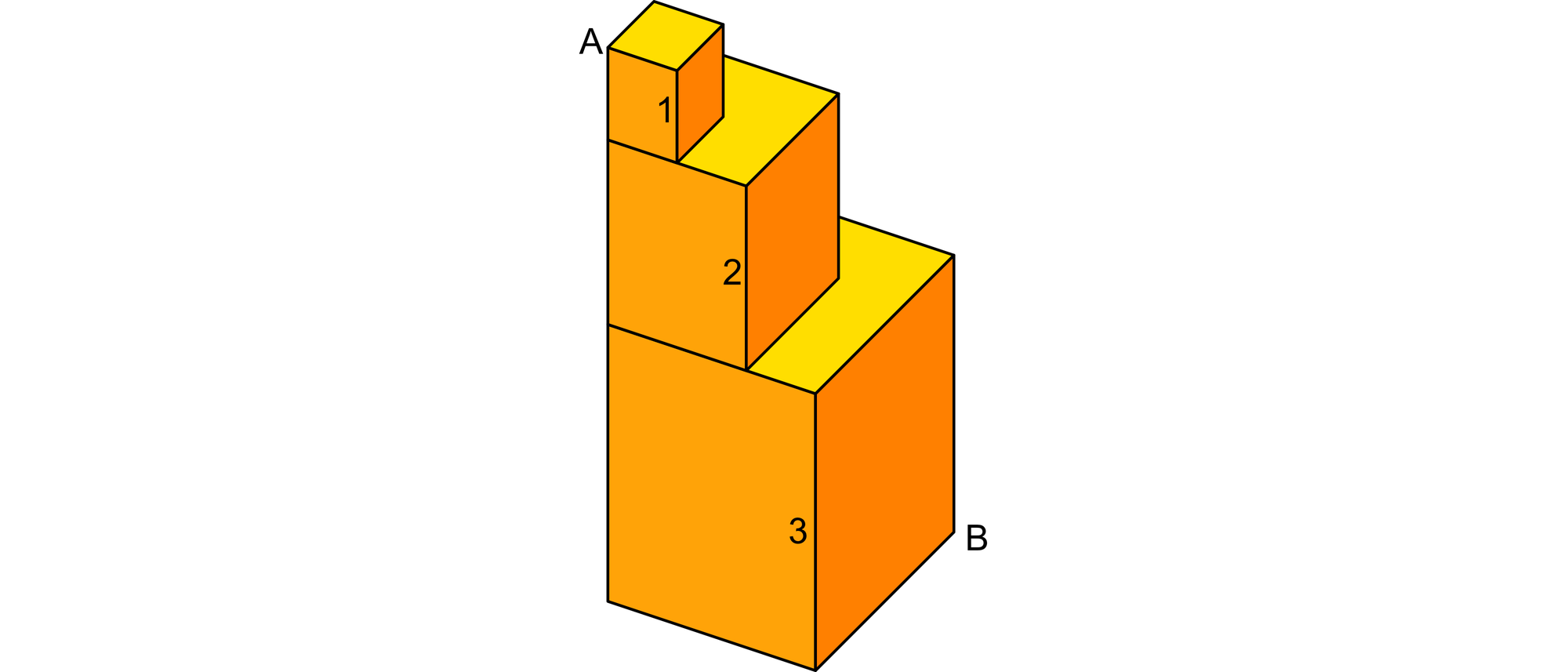
Drei Würfel mit den Kantenlängen von 1, 2 und 3 sind so aufeinander gestapelt worden, wie es die Skizze zeigt. Die beiden Ecken A und B des oberen und des unteren Würfels sind durch eine gerade Linie miteinander verbunden. Wie lang ist der Teil dieser Linie, der durch den mittleren Würfel verläuft?
Das Dreieck AEF ist rechtwinklig, und seine Katheten sind AE = 1 + 2 + 3 = 6 und EF = 3 lang. Mit dem Satz des Pythagoras erhält man damit für die Hypotenuse AF2 = 62 + 32 = 45.
Auch das Dreieck AFB ist rechtwinklig, und sein rechter Winkel liegt am Punkt F. Da die Kathete AF die linke Seitenfläche des mittleren Würfels an der Oberkante betritt und an der Unterkante verlässt, muss die Hypotenuse AB durch die obere Fläche in den mittleren Würfel eindringen und ihn durch die untere Fläche wieder verlassen. Mit dem Satz des Pythagoras ergibt sich für die Hypotenuse AB2 = AF2 + BF2 = 54. Mit dem Strahlensatz kann man nun das gesuchte Stück a der Strecke AB, das im Inneren der zweiten Würfels verläuft, berechnen: a/AB = CD/AE. Daraus ergibt sich a = CD · AB / AE = √6 ≈ 2,449.



Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.