Hemmes mathematische Rätsel: Die beiden Pyramiden
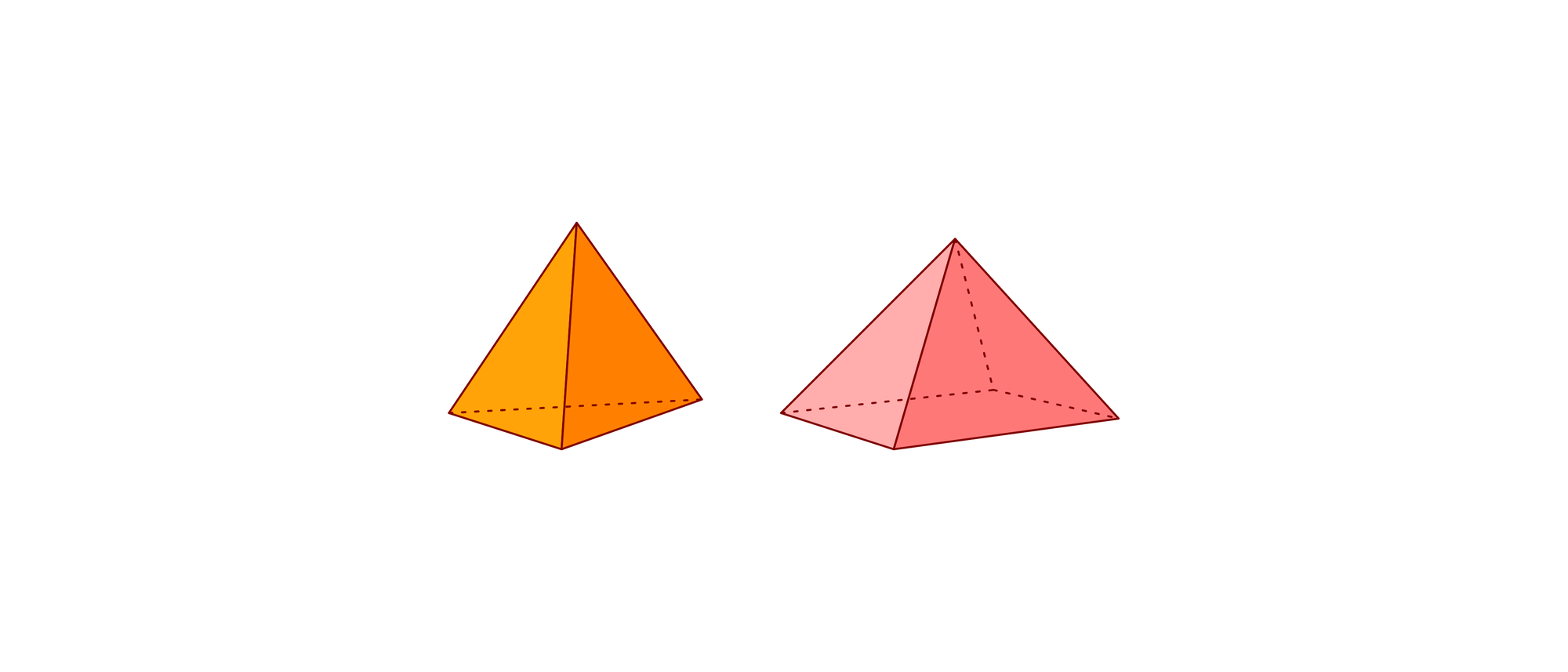
Eine n-seitige Pyramide ist ein Körper mit einer n-eckigen Grundfläche und einem Eckpunkt, der Pyramidenspitze, oberhalb dieser Fläche. Die Pyramidenspitze ist über n dreieckige Mantelflächen mit den n Kanten der Grundfläche verbunden. Ist die Grundfläche ein regelmäßiges n-Eck und liegt die Pyramidenspitze genau senkrecht über dem Mittelpunkt der Grundfläche, nennt man die Pyramide regelmäßig.
Alle Kanten einer regelmäßigen dreiseitigen Pyramide und alle Kanten einer regelmäßigen vierseitigen Pyramide sind zehn Zentimeter lang. Die beiden Pyramiden werden mit zwei ihrer dreieckigen Mantelflächen genau aufeinander geklebt. Wie viele Flächen hat der dadurch entstehende Körper?
Die dreiseitige Pyramide hat vier und die vierseitige hat fünf Flächen. Zwei Flächen verschwinden beim Zusammenkleben, es bleiben also sieben Flächen. Diese Rechnung klingt zwar richtig, ist aber in Wirklichkeit falsch. An zwei Stellen entstehen aus jeweils zwei aneinanderstoßenden Dreiecken Rhomben. Der neue Körper hat deshalb nur fünf Flächen.
Dies kann man ohne jede Rechnung sehen. Die dreiseitige Pyramide ist ein regelmäßiges Tetraeder und die vierseitige die Hälfte eines regelmäßigen Oktaeders. Nun kappen wir von einem regelmäßigen Tetraeder mit einer Kantenlänge von 20 cm die vier Ecken ab, so dass die Kanten des Tetraeders alle halbiert werden. Es bleibt ein regelmäßiges Oktaeder übrig. Dieses Oktaeder wiederum wird zu zwei Pyramiden mit quadratischer Grundfläche halbiert. Da der fünfflächige Körper aus einer Ecke des großen Tetraeders und einer Hälfte des oktaedrischen Mittelstückes besteht, ist somit klar, dass die beiden rhombischen Seitenflächen eben sind und nicht in der Mitte einen Knick besitzen.
Diese Aufgabe wurde in den USA mehrere Jahre lang in einem landesweiten Test gestellt zur Vergabe von Stipendien. Die Prüfer erwarteten als korrekte Lösung die Antwort »sieben Flächen«. Erst 1981 bestand ein Prüfling hartnäckig darauf, dass seine Antwort »fünf Flächen« richtig sein müsse. Eine genaue Überprüfung brachte dann die für die Tester peinliche Wahrheit ans Licht und in die Tagespresse.



Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.