Hemmes mathematische Rätsel: Die Königsberger Brücken
Einer der größten Mathematiker der Welt war Leonhard Euler. Er wurde 1707 in Basel geboren und zog im Alter von 20 Jahren nach St. Petersburg. 1730 erhielt er dort eine Professur für Physik und 1733 für Mathematik. 1741 wurde er von Friedrich dem Großen an die Berliner Akademie berufen, wo er 25 Jahre lang lehrte. 1766 zog er wieder nach St. Petersburg. Er starb 1783. Euler war sehr produktiv und verfasste 866 wissenschaftliche Publikationen. 1735 löste und verallgemeinerte er das Problem der Königsberger Brücken, dass er vermutlich von seinem aus Königsberg stammenden Kollegen Christian Goldbach kennen gelernt hatte.
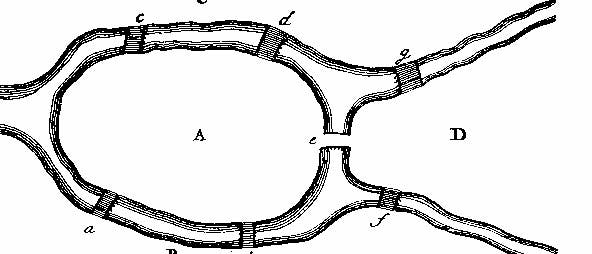
In der Stadt Königsberg umschließen zwei Arme des Pregel die Insel Kneiphof. Sie war im 18. Jahrhundert über sieben Brücken mit den umliegenden Stadtteilen verbunden. Ist es möglich, über jede der sieben Brücken genau einmal zu gehen und dann wieder zum Ausgangspunkt zurückzukehren?
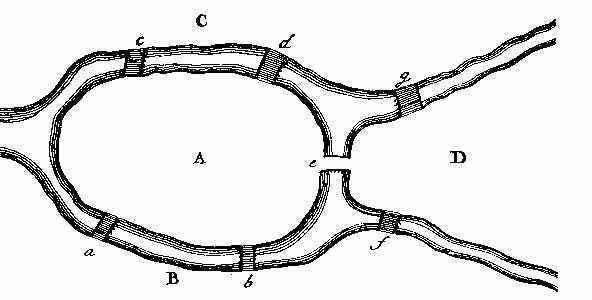
Die Zeichnung stammt übrigens von Euler selbst.
Wir vereinfachen den Stadtplan Königsbergs, indem wir die Stadtteile durch Punkte ersetzen und die Brücken durch Linien, die die Punkte miteinander verbinden.
Wenn man nun über eine Linie in einen Punkt hineinläuft, soll man ihn auch wieder verlassen können. Da keine Linie mehrfach benutzt und auch keine Linie ausgelassen werden darf, muss folglich die Anzahl der Linien, die sich in einem Punkt treffen, geradzahlig sein. Auch vom Startpunkt müssen geradzahlig viele Linien ausgehen, da er ja gleichzeitig Zielpunkt ist. In dem Diagramm enden an jedem der vier Punkte ungeradzahlig viele Linien, und folglich ist das Problem der Königsberger Brücken unlösbar.



Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.