Hemmes mathematische Rätsel: Die Polyominotreppe
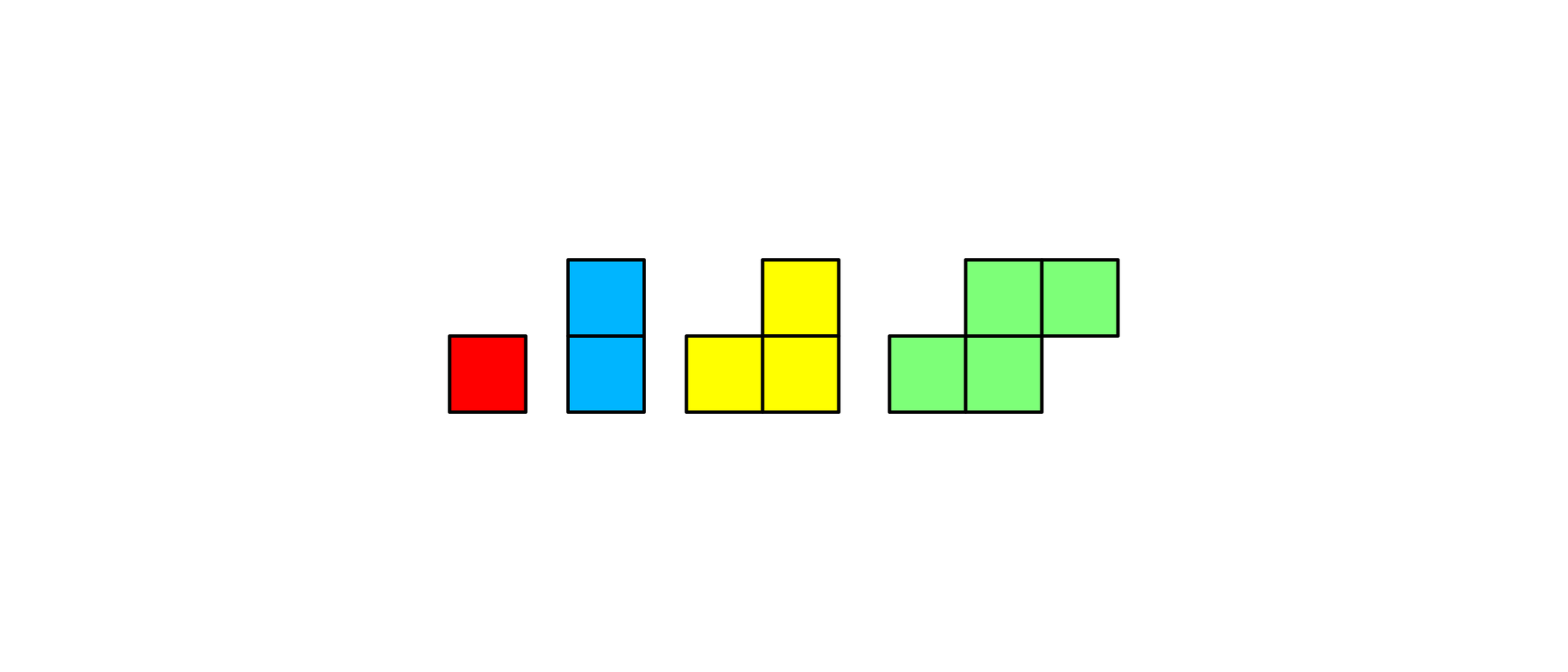
Der amerikanische Künstler, Autor und Puzzle- und Computerspielerfinder Scott Kim wurde 1955 in Washington D. C. geboren. Er ist weltbekannt durch seine meisterhaften Ambigramme, Schriftzüge, die sich, wenn man sie auf den Kopf stellt, nicht ändern. Das folgende Rätsel stammt aus seinem 2014 erschienenen »Little Big Book of Mind Benders«.
Auf wie viele Weisen lassen sie die vier bunten Polyominos zu der treppenförmigen Figur anordnen? Dabei dürfen sie auch umgeklappt werden, so dass die Vorder- zur Rückseite wird.
Liegt das grüne Tetromino so in der Treppe, dass es nur zwei Quadrate hoch ist, kann es vier Positionen einnehmen. Die vierte Position scheidet für eine Lösung aus, da man die drei anderen Polyominos dann nicht mehr unterbringen kann (untere Reihe).
Für die anderen drei Positionen gibt es insgesamt acht Lösungen, die sich leicht durch eine systematische Suche finden lassen (obere zwei Reihen).
Spiegelt man jede Lösung an ihrer von links oben nach rechts unten laufenden Diagonalen, erhält man acht weitere Lösungen, bei denen das Tetromino jeweils so liegt, dass es eine Höhe von drei Quadraten hat.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.