Betrachten Sie kurze Wegstücke, die jeweils eine gleiche Änderung der geografischen – oder wenn Ihnen das besser gefällt: planetografischen – Breite bewirken.

Zunächst die Sache mit der ersten Umrundung: "So geradeaus wie möglich" bedeutet "geodätisch", auf einer Kugel ist das ein Kreis um den Kugelmittelpunkt, genannt "Großkreis". Beide haben also gemeinsam den Planetenumfang zurückgelegt (jeder die Hälfte, wenn sie gleich schnell wandern) und treffen sich an dem Punkt, der dem Start diametral gegenüberliegt. Jedes Stück des Großkreises ist die kürzeste Verbindung auf der Kugel zwischen zwei seiner Punkte – wenn das Stück weniger als eine Hälfte des Großkreises ist.

Die Kurve mit dem konstanten Kurswinkel ist dagegen fast immer ein Umweg zwischen zwei ihrer Punkte, sie heißt "Loxodrome" und erscheint auf der winkeltreuen Zylinderkarte (Mercator-Erdkarte) als (unendlich viele) Geraden, wenn diese äquatorständig ist, und auf der stereografischen Azimutalkarte als logarithmische Spirale, wenn diese Karte polständig ist:

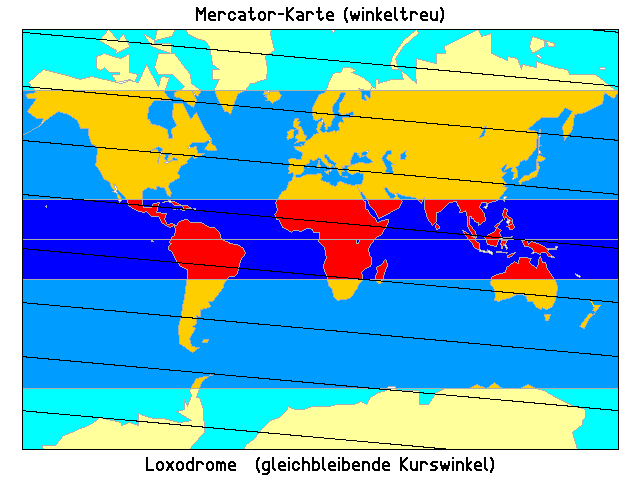
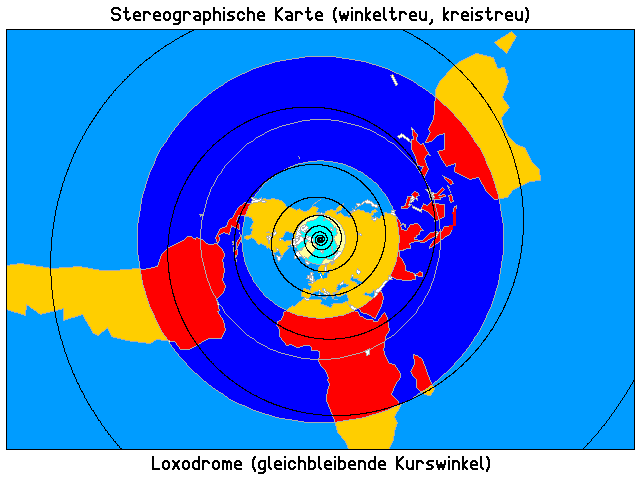
Mit einem Teleobjektiv ("orthografisch") würde sie so aussehen:

Hier ist eine Loxodrome in einem Würfel mit drei Parallelprojektionen auf dessen Seitenflächen zu sehen:

Wir nehmen nun an, dass die benutzten Kompasse die Winkel zu den planetografischen Längengraden anzeigen. (Wenn es Magnetkompasse sind, dann sind die Koordinaten des Planeten auf die Magnetpole zu beziehen; wenn sie, wie erdüblich, auf die Rotationsachse bezogen sind, müssen Eddy und Freddy Kreiselkompasse verwenden. Mit der "Missweisung" der irdischen Magnetkompasse haben wir also nichts zu tun.) Es gibt nun drei Fälle: Wenn Eddy und Freddy in Richtung zu den Polen starten, kommt jeder an einem der beiden Pole an und muss dort stehenbleiben, denn der Kompass gibt ihm keine Richtung zum Weitergehen an. Wenn einer von beiden einfach geradeaus über den Pol gehen würde, wäre das auf dem Kompass die Gegenrichtung zu vorher. Beide laufen also zusammen einen halben Planetenumfang. Wie viel jeder zur Gesamtlaufstrecke beiträgt, hängt von der planetografischen Breite des Startortes ab.

Wenn sie genau nach Westen bzw. Osten starten, so laufen sie auf einem gemeinsamen Breitenkreis und begegnen sich wieder, im Falle des Äquators wie beim Großkreis (welch Wunder: der Äquator ist ein Großkreis), in den übrigen Fällen schon nach kürzeren Wegen (der Faktor ist der Cosinus des Breitenwinkels).

Es bleiben noch alle anderen Kurswinkel übrig, und mit diesen enden die Wege von Eddy und Freddy an den beiden Polen, die jeder von ihnen unendlich oft umrundet (jedenfalls theoretisch).

Sind auch ihre Wege unendlich lang?

Die ganze Loxodrome (also die Wege von beiden zusammen) läuft von einem Pol zum anderen, durchläuft also alle planetografischen Breiten von –90^o bis +90^o. Jedes kleine Stückchen der Loxodrome ersetzt also ein Wegstückchen in Nord-Süd-Richtung und eins in Ost-West-Richtung, mit diesen bildet es Dreieck mit stets den gleichen Winkeln, nämlich dem Kurswinkel, einem rechten Winkel und dem Rest, zusammen fast genau 180^o, denn wir nehmen so kleine (sozusagen unendlich kleine) Stückchen, dass die Kugelwölbung vernachlässigbar ist. Die Summe der nord-südlichen Stücke ist natürlich der halbe Planetenumfang, die der anderen verhalten sich dazu wie die Seiten des betrachteten Dreiecks. Die Loxodrome hat also von Pol zu Pol eine endliche Länge, wenn der Betrag des Kurswinkels gegen den Meridian kleiner als 90^o ist (wenn er gleich 90^o ist, kommt sie nie zum Pol, sondern bleibt auf ihrem Breitengrad); allgemein muss man den halben Planetenumfang durch den Cosinus dieses Winkels teilen.