Drachen falten

Nehmen Sie bitte einen langen Papierstreifen und markieren ein Ende mit einem Kreuz. Halten Sie dann den Streifen so vor sich, dass das Kreuz links ist. Falten Sie den Streifen so, dass das rechte Ende genau hinter dem linken Ende mit dem Kreuz ist. Wiederholen Sie dieses Falten so oft, wie die Papiermaße es zulassen, das heißt, klappen Sie immer das jeweils rechte Ende hinter das Kreuz links. Entfalten Sie das Papier und ziehen Sie es so weit auseinander, dass alle Falten ungefähr zu rechten Winkeln werden. Das sieht dann ungefähr so aus wie im Bild oben.
Wie wechseln sich Berg- und Talfalten ab?
Stellen Sie sich vor, das Papier hätte auf der Rückseite eine andere Farbe. Dann würden Sie sehen, dass das Papier Ihnen nach einigem Falten stellenweise seine Rückseite zuwendet, wenn auch durch andere Teile verdeckt, die die Vorderseite zeigen. Was von vorn wie eine Bergfalte aussieht, erscheint beim Blick auf die Rückseite als Talfalte und umgekehrt.
Die erste Faltung ist eine Bergfalte B, mitten auf der Länge. Wenn Sie diese ans linke Ende klappen und in der bisherigen Mitte wieder falten, bekommt die linke Hälfte eine Bergfalte B, die rechte aus Ihrer Sicht auch. Aber da sie rückwärts liegt, ist das nach dem Abwickeln eine Talfalte T. Wir haben also dann von links (Anfang A ) nach rechts (Ende E ) 5 Punkte in jeweils 1/4 der Länge als Abstand: ABBTE.
Faltet man den Streifen ein weiteres Mal, findet man in jeweils 1/8 Abstand weitere Falten, abwechselnd Berg und Tal: ABBTBBTTE.
Das Schema ist folgendes:
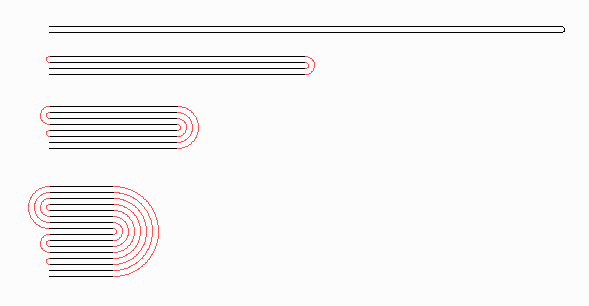
A---------------B---------------E
A-------B-------B-------T-------E
A---B---B---T---B---B---T---T---E
A-B-B-T-B-B-T-T-B-B-B-T-T-B-T-T-E
ABBTBBTTBBBTTBTTBBBTBBTTTBBTTBTTE
Dabei folgen nie mehr als drei Falten der gleichen Art aufeinander. Wenn man nun jede Falte zu einem rechten Winkel abwickelt, Berg- und Talfalten durch Rechts- und Linkskurven ersetzt und das Papier so auf den Tisch legt, dass seine Unterkante eine Kurve auf dem Tisch beschreibt, dann trifft diese Kurve manche Punkte doppelt, überkreuzt sich aber nirgends (wie auch, Papier durchdringt sich ja nicht selbst). In der Animation sind die Ecken durch Andeutungen von Abrundungen ersetzt (nämlich mit Achteck-Winkeln):
Das detaillierteste Bild, das die Bildschirmauflösung hergibt, zeigt einen schönen chinesischen Drachen:

Beachten Sie, dass die beiden verschieden gefärbten Hälften genau identisch mit dem jeweils vorhergehenden Bild sind, dass also der Drachen – abgesehen von der zunehmenden Verfeinerung – im geometrischen Sinn ähnlich zu seinen beiden Hälften ist. Da diese aber sehr raffiniert ineinander greifen, ist das ohne den Färbung kaum zu sehen. Vielmehr scheint er mit seiner Wespentaille in zwei ungleiche Teile zu zerfallen:

Betrachten wir aber den Übergang von einer Faltung zur nächsten, so wird jedes Mal eine Strecke (blau) durch einen rechtwinkligen Streckenzug aus zwei gleichen Teilen ersetzt (rot), der abwechselnd (in Fahrtrichtung) nach rechts und nach links orientiert ist:

Was geschieht, wenn wir beim Falten das rechte Ende abwechselnd von vorne und von hinten an das linke Ende anbringen, also statt dieser Legung

diese vornehmen?
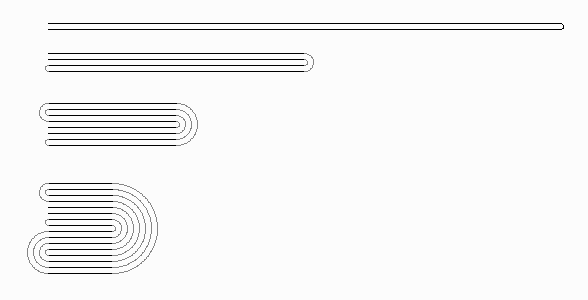
Das Ergebnis ist viel nüchterner, aber nicht weniger verblüffend: Ein Dreieck wird immer feiner durch eine einzige Linie ausgefüllt. Obwohl das auch auf den Drachen zutrifft, sieht man an diesem Beispiel noch deutlicher, dass es sich um ein zweidimensionales Fraktal handelt! Auch die Selbstähnlichkeit ist nun wirklich nicht zu übersehen.



Schreiben Sie uns!
Beitrag schreiben