Hemmes mathematische Rätsel: Dreieck, Sechseck und Kreis
Abu l-Hasan Thabit ibn Qurra ibn Sahrun al-Harrani wurde 836 geboren und starb 901. Er war ein bedeutender Mathematiker, Astronom und Arzt, aber er beschäftigte sich auch mit philosophischen, physikalischen und geographischen Fragen. Er übersetzte griechische und syrische Schriften ins Arabische und kommentierte sie. Thabit ibn Qurra hat auch etliche unterhaltsame Probleme aus der Geometrie in seinen Schriften veröffentlicht.
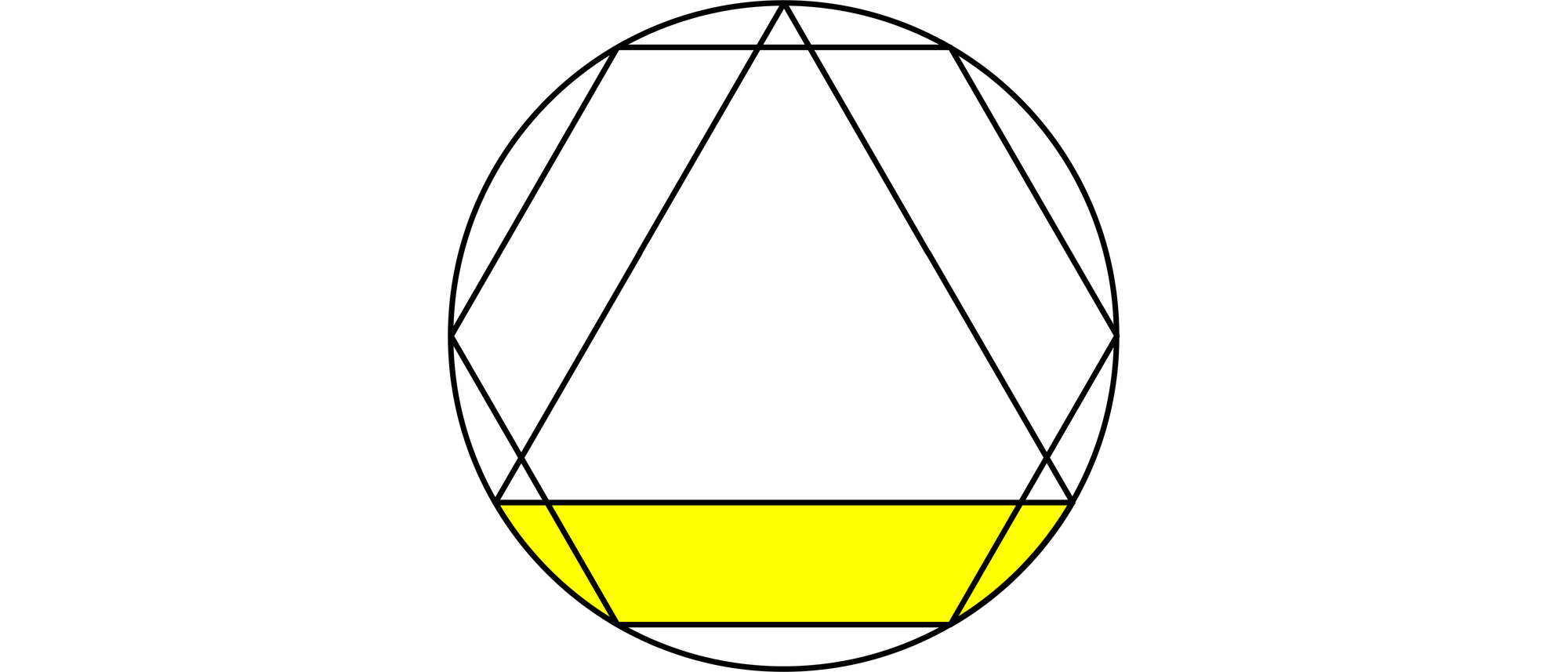
In einen Kreis werden ein gleichseitiges Dreieck und ein regelmäßiges Sechseck so eingezeichnet, wie die Abbildung es zeigt. Die untere Dreieck- und die untere Sechseckseite schneiden aus dem Kreis den gelb unterlegten Streifen heraus. Den wievielten Teil der Kreisfläche nimmt der gelbe Streifen ein?
Dreht man das Sechseck in dem Kreis um 30 Grad und verbindet seine Ecken mit dem Kreismittelpunkt, so sieht man, dass es sich aus zwölf gleichen kleinen, rechtwinkligen Dreiecken zusammensetzt. Das gleichseitige Dreieck hingegen besteht nur aus sechs dieser kleinen Dreiecke. Die Sechseckfläche ist also doppelt so groß wie die Fläche des gleichseitigen Dreiecks.
Den gelben Streifen kann man in der Zeichnung noch zwei weitere Male finden. Die Gesamtfläche 3F der drei Streifen erhält man, indem man von der Kreisfläche K die drei Kreisabschnitte A und die Fläche D des gleichseitigen Dreiecks abzieht: 3F = K − 3A − D.
Zieht man von der Kreisfläche die Sechseckfläche S ab, so bleiben sechs Kreisabschnitte übrig, die die Fläche 6A = K − S haben. Teilt man diese Gleichung durch 2 und setzt sie in die erste ein, ergibt sich 3F = K − (K − S)/2 − D = K/2 + S/2 − D. Da nun D = S/2 ist, heben sich die beiden letzten Summanden gegenseitig auf und es bleibt 3F = K/2 oder F = K/6 übrig. Folglich nimmt ein gelber Streifen ein Sechstel der Kreisfläche ein.



Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.