Die blauen und roten Zahlen zeigen das Pascal-Dreieck, in dem jede Zahl die Summe der beiden Zahlen ist, die nach oben duch die hellblauen Linien mit ihr verbunden sind; an den Rändern links und rechts stehen überall Einsen.

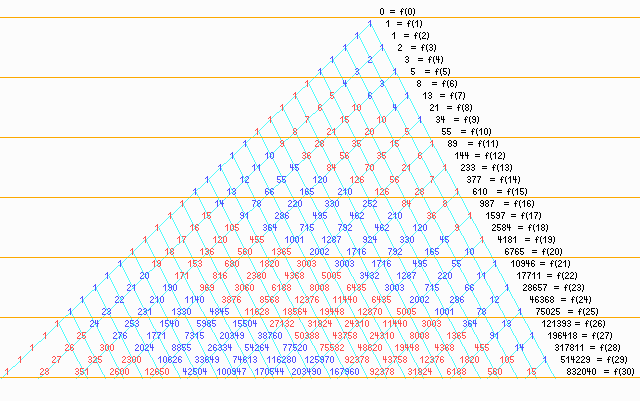
Normalerweise schreibt man diese Zeilen waagerecht. Hier sind sie nach rechts etwas abschüssig gemacht, die Farben Rot und Blau zeigen die übliche Zeilenstruktur des Pascal-Dreiecks. Wenn man in jeder solchen Zeile mit der Nummer n (angefangen mit n = 0) die Summe bildet, kommt die Potenz 2ⁿ heraus. Der Grund ist einfach der, dass jede Zahl zweimal als Summand aufgerufen wird, allerdings außer den Einsen am Rand: Sie kommen nur einmal dran, aber dafür kommt in jeder Zeile eine neu hinzu.

Bei unserer Schiefstellung des Pascal-Dreiecks stehen in jeder Zeile Zahlen, die Summen aus solchen der beiden oberen Nachbarzeilen sind, wobei jeder Summand einmal aufgerufen wird. Für die Summen der Zahlen in je einer Zeile gilt also, dass sie jeweils die Summen der Zahlen aus den beiden nächsthöheren sind. Die Zeilensummen bilden also eine verallgemeinerte Fibonacci-Folge mit der Bedingung a_n = a_n–2 + a_n–1.

Wie man ablesen kann, sind die Startwerte dabei die der Fibonacci-Folge, nämlich f(1) = 1 und f(2) =1. Die Fibonacci-Folge tritt also im Pascal-Dreieck in den Summen über schräg laufende Zeilen auf, die wir hier aber in die Waagerechte geschert haben.