Flaggenmasten

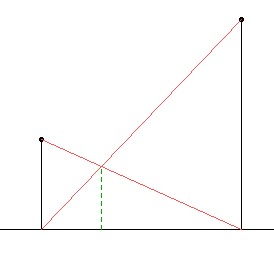
Auf dem Rathausplatz stehen zwei Flaggenmasten, einer 7 m hoch, der andere 3 m hoch. Von der Spitze des einen geht ein stramm gespannter Draht zum Fuß des anderen, und umgekehrt ebenfalls. In welcher Höhe (über dem ebenen, waagerechten Platz) kreuzen sich die Drähte? Wir nehmen natürlich an, dass die Flaggenmasten völlig senkrecht stehen und unmessbar dünn sind, und dass die Drähte überhaupt nicht durchhängen (alles mehr denkaufgaben-freundlich als realistisch).
Diese (leichte) Aufgabe hat noch eine schwere Schwester, die fast genau so aussieht, aber in der die schrägen Längen eine Rolle spielen.
Wenn man zweimal einen Strahlensatz anwendet, kommt man auf die gesuchte Höhe \(h = ab/(a + b)\), wobei \(a\) und \(b\) die Längen der beiden Flaggenmasten sind.
Es mag vielleicht erstaunen (wie auch Dudeney anmerkt), dass der Abstand der Masten voneinander keine Rolle spielt, sondern sich in der Rechnung wegkürzt.
Wir haben also ein Ergebnis, das nur von \(a\) und \(b\) abhängt, stets zwischen \(a/2\) und \(b/2\) liegt und für \(a = b\) auch genau so groß ist wie \(a/2 (=b/2)\). Das kennen wir doch von Mittelwerten!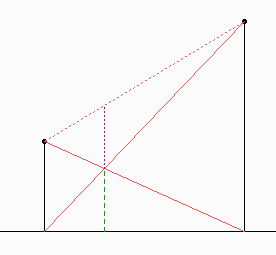
Tatsächlich ist \(h\) nichts anderes als die Hälfte des harmonischen Mittels aus \(a\) und \(b\), das als \(m_h = 2ab/(a + b) \) definiert werden kann, oder auch geometrisch als Parallele durch den Schnittpunkt der Diagonalen eines Trapezes mit den zueinander parallelen Seiten \(a\) und \(b\). Die geometrische Definition liefert auch eine elegante Methode zur zeichnerischen Bestimmung des harmonischen Mittels.



Schreiben Sie uns!
Beitrag schreiben