Hemmes mathematische Rätsel: Fünf Punkte im Dreieck
Der Wissenschaftsjournalist Greg Ross betreibt seit 2005 eine Internetseite mit dem Titel »Futility Closet«, die er als eines Müßiggängers Sammlung von kurz gefasstem Zeitvertreib bezeichnet. Seine Sammlung enthält mehr als 10 000 Kuriositäten aus den Bereichen Geschichte, Literatur, Sprache, Kunst, Geografie, Philosophie und Mathematik. Darunter ist auch ein Schatz von über 1000 Denksportaufgaben. Ross' Sammlung wächst von Tag zu Tag und inzwischen sind auch zwei Bücher daraus entstanden. Im April 2012 veröffentlichte er folgendes Problem:
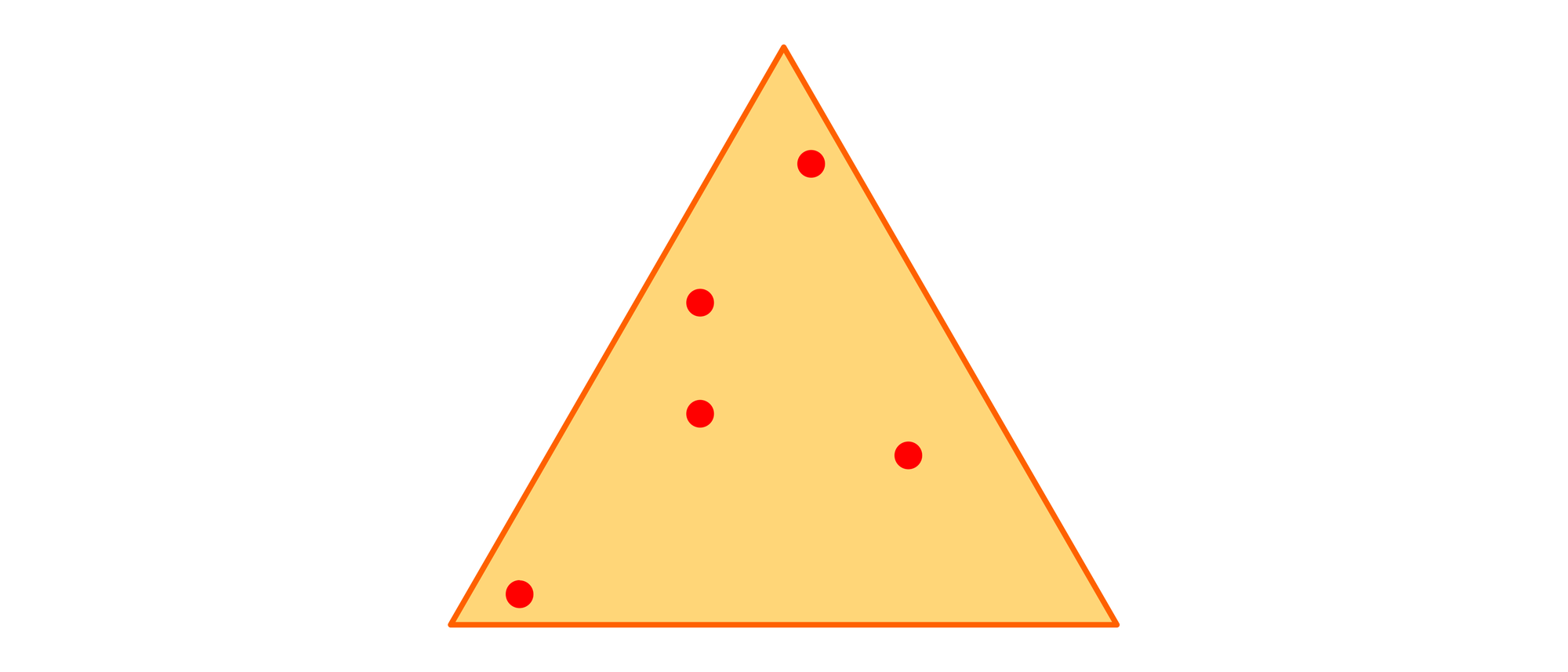
In ein gleichseitiges Dreieck der Seitenlänge 1 werden ganz zufällig fünf Punkte eingezeichnet. Wie groß kann der Abstand der beiden Punkte, die sich am nächsten liegen, höchstens sein?
Wir teilen das gleichseitige Dreieck in vier kleine gleichseitige Dreiecke mit den Seitenlängen 1⁄2 auf. Wenn wir jetzt die fünf Punkte über das große Dreieck verteilen, müssen wenigstens in einem der vier kleinen Dreiecke mindestens zwei Punkte liegen. Zwei Punkte innerhalb eines kleinen Dreiecks können aber keinen größeren Abstand voneinander haben als 1⁄2. Dieser größtmögliche Abstand wird erreicht, wenn die beiden Punkte auf zwei Ecken des Dreiecks liegen. Nur wenn alle fünf Punkte auf den Ecken oder den Seitenmittelpunkten des großen Dreiecks liegen, gibt es kein Punktepaar, dessen Abstand kleiner ist als 1⁄2.



Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.