Drehen Sie die Erde in Gedanken ein halbes Mal um ihre Achse.

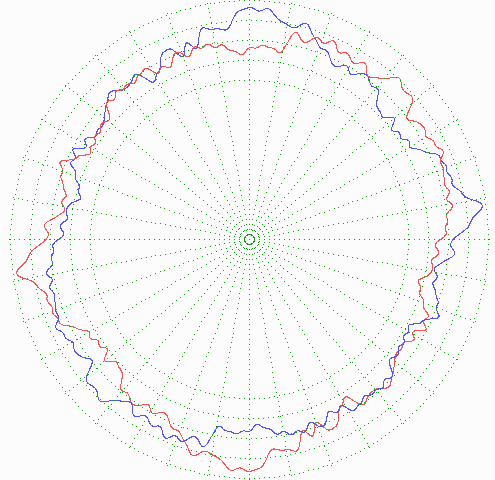
Das Bild zeigt eine ziemlich wilde Höhenverteilung auf dem Äquator in Blau und dieselbe Höhenverteilung um eine halbe Drehung versetzt in Rot. Beide Kurven müssen sich mindestens einmal schneiden. Das sind die Stellen, die genau so hoch sind wie die diametral gegenüberliegenden.

Das ist der Satz von Borsuk und Ulam in seiner Version für eine geschlossene Linie. In zwei Dimensionen erscheint er bei weitem nicht so selbstverständlich: Auf der Erdoberfläche (als geschlossener Fläche) gibt es mindestens zwei diametral gegenüberliegende Punkte (die also mit einer Geraden duch den Erdmittelpunkt verbunden sind), an denen zwei stetige ortsabhängige Funktionen, z. B. Temperatur und Luftdruck ,übereinstimmen (wohlgemerkt: dieselben beiden Punkte für beide Messgrößen).

Die zackige Kurve habe ich übrigens mit einer Fourier-Reihe zeichnen lassen, bei der die Amplituden der 100 Teilschwingungen mit dem Kehrwert der Frequenzen gehen und die Phasenlagen zufällig sind (sonst gäbe es einen Sägezahn).