Goldener Schnitt im Zehneck

© iStock / nicolas (Ausschnitt)
Beweisen Sie: Im regelmäßigen Zehneck verhält sich die 3 Seiten überspannende Diagonale zum Umkreisradius wie der goldene Schnitt, d. h. wie die Diagonale zur Seite im regelmäßigen Fünfeck.
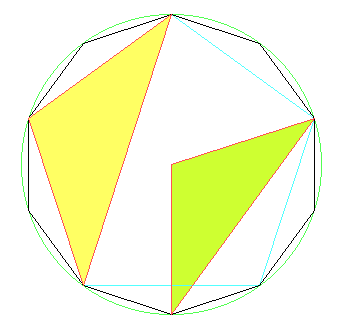
Die getönten Dreiecke sind gleichschenklig, haben den stumpfen Winkel 108o gemeinsam und sind daher ähnlich zueinander.



Schreiben Sie uns!
Beitrag schreiben