Hemmes mathematische Rätsel: Gurami
Die beiden Mathematiker Klaus-Peter Rudolph und Hans-Friedrich Bauch aus Mecklenburg-Vorpommern haben vor einigen Jahren eine neue Art von Rätseln erfunden, die sie Guramis nennen und die eine gewisse Ähnlichkeit mit Sudokus haben. 2011 veröffentlichten sie in Berlin ein Buch mit dem Titel »Gurami – das neue Zahlenrätsel«, das 60 dieser Aufgaben enthält.
Ein Gurami ist ein Raster aus dreieckigen Feldern, die entweder rot oder grün sind. In dem Raster liegen die Dreiecke auf Streifen, die waagerecht verlaufen oder die von links nach rechts aufsteigen oder die von links nach rechts absteigen. Um diese Struktur zu verdeutlichen, sind die Streifen in der Skizze für alle drei Fälle auseinandergezogen worden.
In die Felder des Guramis sollen Zahlen so gesetzt werden, dass anschließend sowohl in den roten als auch in den grünen Feldern alle Zahlen von 1 bis 8 je einmal auftauchen. Außerdem muss in jedem Streifen die Summe der Zahlen auf den roten Feldern gleich der Summe der Zahlen auf den grünen Feldern sein.
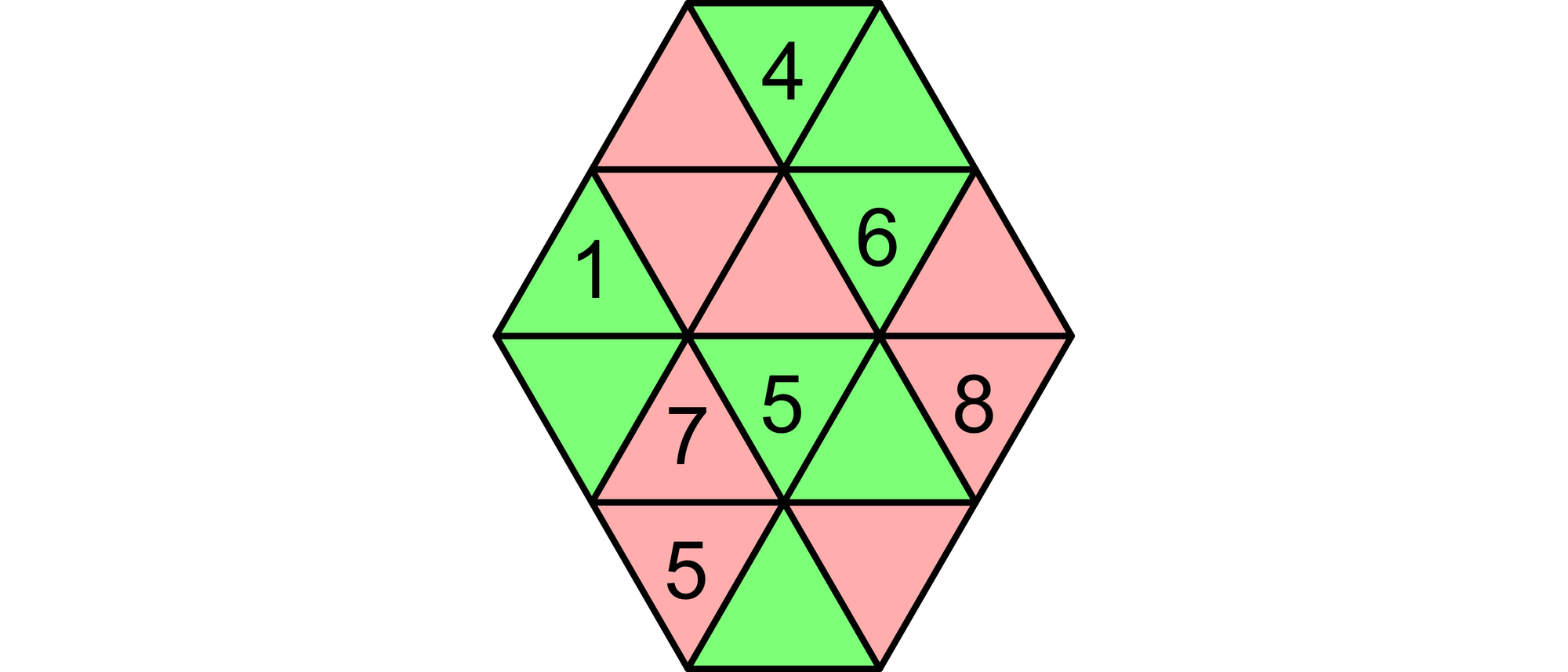
In dem Gurami sind schon einige Zahlen vorgegeben. Versuchen Sie, die restlichen Felder zu füllen.
Im zweiten aufsteigenden Streifen steht auf den roten Feldern bereits 7 + 5 = 12 und auf den grünen 5 + 6 = 11. Die Zahl auf dem noch freien grünen Feld dieses Streifens muss also um 1 größer sein als die Zahl auf dem noch freien roten Feld. Hierfür kommen nur noch die beiden Zahlenpaare (2,1) und (3,2) in Frage. Setzt man die 1 in das freie grüne Feld, folgt daraus, dass im dritten absteigenden Streifen auf dem freien roten Feld eine 5 stehen muss. Diese steht aber schon auf einem anderen Feld. Folglich muss nicht die 1, sondern die 2 auf dem freien grünen Feld des zweiten aufsteigenden Streifens stehen.
Dadurch liegen auch die 1 im zweiten aufsteigenden und die 4 im dritten absteigenden Streifen eindeutig fest. Nun ist im zweiten horizontalen Streifen nur noch ein rotes Feld frei, in das man die 2 setzen muss. Anschließend ist es sehr einfach, die restlichen Zahlen auf die noch freien Felder zu verteilen.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.