Harts Inversor

Das ist ein Antiparallelogramm, also ein ebenes Viereck, das aus den Schenkeln und den Diagonalen eines gleichschenkligen Trapezes gebildet wird oder durch Überschlagen eines Parallelogramms.
Wir verformen die Figur mit festen Seitenlängen nun in dem Bereich, in dem die langen Seiten sich noch kreuzen, und stellen dabei zweierlei fest:
1. Die Mitten aller Seiten des Antiparallelogramms liegen immer auf einer gemeinsamen Geraden;
2. Zwei der Abstände zwischen den Seitenmittelpunkten haben ein konstantes Produkt:
Warum ist das so, und wie kann man das benutzen, um einen Punkt allein mit Drehgelenken auf einer Geraden zu führen?
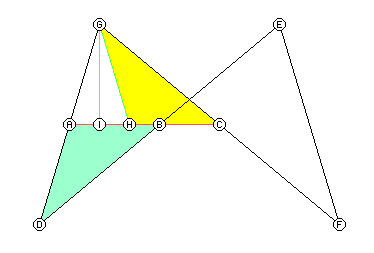
DEFG ist das Antiparallelogramm, A, B und C sind die Mitten der drei Seiten GD, DE und FG. Nach Voraussetzung ist DFEG ein Trapez, also sind dessen Seiten DF und EG parallel zueinander, und die Mittelparallele zu beiden halbiert nach Strahlensatz jede Seite des Antiparallelogramms.
Die Strecke GI ist das Lot von G auf AC, und IH ist so lang wie AI. Dann sind die beiden getönten Dreiecke (mit Klappung) deckungsgleich zueinander und es gilt: AB = HC und damit AH = BC.
Wir interessieren uns für AB\(\cdot\)AC = HC\(\cdot\)AC = HC\(\cdot\)(HC + 2·IH). Das kann weiter vereinfacht werden, indem man nutzt: HC + IH = IC. Dann folgt: AB\(\cdot\)AC = IC2 – IH2.
Wenden wir den Satz des Pythagoras an den Dreiecken IHG und ICG an, finden wir, dass das Produkt AB\(\cdot\)AC = CG2 – AG2 ist, also nur von den Längen der Seiten des Antiparallelogramms und nicht von den Winkeln abhängt.
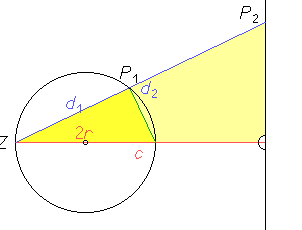
In diesem Bild haben die Punkte P1 und P2 von Z (auf dem Kreis) die Abstände d1 bzw. d2. Beide Dreiecke in der Abbildung sind ähnlich zueinander, sodass: \(\frac{2r}{d_2}=\frac{d_1}{c}\)
Das Produkt beider Abstände d1 und d2 ist also 2rc und damit nur vom Radius des Kreises und vom Abstand c – 2r der Geraden vom Kreis abhängig. Das ist ein Spezialfall der "Inversion" oder auch "Spiegelung am Kreis" (die aber nur wenig mit der optischen Spiegelung zu tun hat): Das Bild eines Kreises unter der Inversion ist wieder ein Kreis. Der abzubildende oder der abgebildete Kreis (oder beide) kann dabei zu einer Geraden "entarten".

Um mit dem Antiparallelogramm eine exakte Geradführung zu erreichen, führt man daher die Mitte einer Seite (Punkt B im Video) auf einem Kreis, der durch die Mitte einer anderen Seite (Punkt A) geht: eine der verbleibenden Seitenmitten (C) läuft dann auf einer Geraden.
Zwar kann natürlich nur ein Teil der (unendlich langen!) Geraden durchlaufen werden und daher auch nur ein Teil des Kreises, aber die Führung ist theoretisch exakt, d.h. ist nur so ungenau wie die Maßhaltigkeit der Stangen und Achsen in ihnen.
Das hat der Hartsche Inversor mit dem von Peaucellier gemeinsam: Im Gegensatz zu der exakten Geradführung von Sylvester und Kempe benutzen beide die Inversion. Genauer: B und C sind Bilder voneinander unter der Inversion am festen Kreis (der durch A geht).




Schreiben Sie uns!
Beitrag schreiben