Hoch 5

Denken Sie sich eine natürliche Zahl \(n\) und nehmen Sie deren 5. Potenz, notfalls mit Taschenrechner.
– Habe ich.
Nun ziehen Sie die gleiche Zahl \(n\) davon ab und teilen das Ergebnis durch 5.
– Ja, und?
Finden Sie es selbstverständlich, dass so etwas ohne Rest aufgeht?
Geht das auch mit anderen Zahlen statt der 5? Ist also \(n^p-n\) immer durch \(p\) teilbar? Oder können Sie eine Sorte von Zahlen \(p\) angeben, für die es geht? Wenn Sie den Beweis zunächst für \(p = 5\) führen, können Sie darauf kommen.
Dieser Schluss von \(n\) auf \(n+1\) mit Verankerung wird auch als Induktionsbeweis oder "vollständige Induktion" bezeichnet, in Anspielung auf die in den Naturwissenschaften übliche Induktion, die eine logisch nicht gerechtfertigte, aber statistisch sinnvolle Verallgemeinerung vieler Einzelbeobachtungen ist.
Nun zu unserer (logisch einwandfreien!) Verallgemeinerung von 5 auf auf andere Zahlen: Bei der Ausrechnung von \((n + 1)^p\) tauchen alle Potenzen von \(n\), von \(n^p\) bis \(n^0\), mit gewissen Faktoren auf, die auf den schönen Namen "Binomialkoeffizienten" hören. Im Falle \(p = 5\) haben sie die Werte 1 5 10 10 5 1 (in dieser Reihenfolge, wie wir gesehen haben) .
Der erste und der letzte sind (immer) 1 (warum?), und die anderen sind bei \(p = 5\) durch 5 , also durch \(p\) teilbar, wie wir zu unserer Freude gesehen haben.
Wenn wir nun nach anderen Zahlen \(p\) suchen, für die ebenfalls \(n^p-n\) für alle natürlichen Zahlen \(n\) durch \(p\) teilbar ist, sind wir gut bedient, wenn für eine Potenz \((n + 1)^p\) alle Binomialkoefizienten außer dem nullten und dem letzten (die stets 1 sind) durch \(p\) teilbar sind.
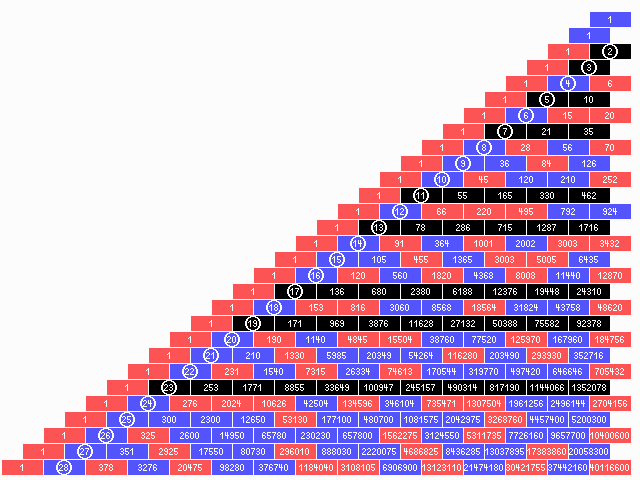
Wenn man sich im pascalschen Dreieck (das alle Binomialkoeffizienten übersichtlich aufführt) umsieht, kommt einem ein Verdacht: Wenn \(p\) eine Primzahl ist könnte es klappen.
| p=0 | . | 1 | . | |||||||||||||
| p=1 | . | 1 | 1 | . | ||||||||||||
| p=2 | . | 1 | 2 | 1 | . | |||||||||||
| p=3 | . | 1 | 3 | 3 | 1 | . | ||||||||||
| p=4 | . | 1 | 4 | 6 | 4 | 1 | . | |||||||||
| p=5 | . | 1 | 5 | 10 | 10 | 5 | 1 | . | ||||||||
| p=6 | . | 1 | 6 | 15 | 20 | 15 | 6 | 1 | . | |||||||
| p=7 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | ||||||||
Nun kann man diese Binomialkoefizienten auch mit der Funktion "Fakultät" ausdrücken, die als Ausrufezeichen geschrieben wird, weil sie so eindrucksvoll große Ergebnisse liefern kann. \(a!\) bedeutet dabei für \(a>0\) das Produkt aller positiven ganzen Zahlen von 1 bis \(a\), und im Falle 0 ist 0! = 1 festgelegt.
Für \((n + 1)^p\) schreiben sich dann die \(n + 1\) Koeffizienten der Reihe nach mit zunehmender Nummer \(k\) als \(p!/(k!(p – k))!\). Nun sieht man sofort, dass für \(k=0\) und \(k=1\) jeweils 1 herauskommt und dass bei den anderen Wetren von \(k\) für Primzahlen \(p\) im Zähler ein \(p\) als Faktor übrigbleibt, der durch nichts im Nenner weggekürzt werden kann.
Es gilt also der Satz:
Ist \(p\) eine Primzahl und \(a\) eine natürliche Zahl, so ist \(a^p – a\) durch \(p\) teilbar (ohne Rest, was in solchen Fällen immer gemeint ist).
Ein Beispiel, das man gerade noch fast im Kopf rechnen kann: \(2^{11} – 2 = 2048 – 2 = 2046 = 11 \cdot 186\).
Für den Spezialfall \(p = 5\) (der in den meisten Rätselbüchern als einziger behandelt wird) gibt es noch einen weniger vornehmen Beweis, der das Ziffernsystem der Basis 10 benutzt: Wie es der Zufall so will (ob man in der Zahlentheorie überhaupt von Zufall reden soll, ist eher ungewiss), geben alle 10 Endziffern in der 5. Potenz wieder die gleiche Endziffer, und wenn man dann die gleiche Zahl wieder abzieht, bekommt man etwas mit der Endziffer 0, und das ist (im Dezimalsystem wohlgemerkt) durch 5 teilbar.
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
0 | 1 | 32 | 243 | 1024 | 3125 | 7776 | 16807 | 32768 | 59049 |
Natürlich muss man diese Zahlen nicht wirklich ausrechnen, um das mit den Endziffern zu sehen.
Die hier behandelte Aussage ist eine der möglichen Formulierungen des "kleinen Satzes von Fermat". Gelegentlich hat Pierre de Fermat (1607–1665) Behauptungen aufgeschrieben und so getan, als hätte er die Beweise gehabt und wieder verloren. Bei dem "großen" oder "letzten" Satz hat es bis 1995 gedauert, bis ein richtiger Beweis gefunden wurde (Satz von Wiles: Fermats als "letzter Satz" bekannte Vermutung trifft zu).
Der "kleine Satz von Fermat" aus dem Jahre 1640, mit dem wir es hier zu tun haben, musste "nur" knapp 100 Jahre auf den (erneuten?) Beweis (durch Euler) warten. Dabei ist er eigentlich ziemlich leicht zu beweisen, wie wir gesehen haben. In Büchern über Algebra oder Zahlentheorie kommt er ziemlich weit vorne vor und erscheint dann vor dem Hintergrund algebraischer Begriffsbildungen ("Restklassenring" und so etwas) als einfache Folgerung der Anfangsgründe.
Ich bin aber mit Algebra so wenig vertraut, dass ich zwar von diesem Satz gehört hatte, aber beim Beweis der Denkaufgabe mit der 5. Potenz und ihrer Verallgemeinerung nicht wusste, dass es genau dieser Satz war. So habe ich einen Kollegen vom Mathematik-Fachbereich gefragt, was das für ein Satz sei. Zu meinem nachträglichen Trost fiel es ihm nicht auf Anhieb ein, und er verwies mich an einen Kollegen, der Spezialist für Algebra ist. Der mailte mir dann wenige Minuten später die Sachlage, und mit dem Such-Stichwort Fermat fand ich selbst in meinen algebra-armen Bücherregalen einiges.
Ross Honsberger behandelt das Thema in seinen "Mathematischen Edelsteinen" gleich im 1. Kapitel sehr lehrreich. So findet man dort auch Interessantes zur Frage der Umkehrbarkeit. Auf die Binomialkoeffizienten bezogen, heißt das: Ist \(n\) eine Primzahl, wenn alle Binomialkoeffizienten von \( {n \choose 1} = {n! \over (n-1)!}= n\) bis \( {n \choose n-1} = {n! \over (n-1)!}= n\) durch \(n\) teilbar sind? Meistens ja, aber nicht immer. Die Gegenbeispiele werden zur Belohnung zu "absoluten Pseudo-Primzahlen" ernannt. Die kleinste unter ihnen ist \( 561 = 3 \cdot 11 \cdot17\).In diesem Bereich der ersten 29 Zeilen des Pascal-Dreiecks treten sie noch nicht auf. Die schwarzen (in den Zeilen mit Primzahlen als Nummern) und blauen Felder (in den übrigen Zeilen) zeigen die Binomialkoeffizienten, die durch die Nummer der Zeile teilbar sind, rot die nicht teilbaren.



Schreiben Sie uns!
Beitrag schreiben