Kovner
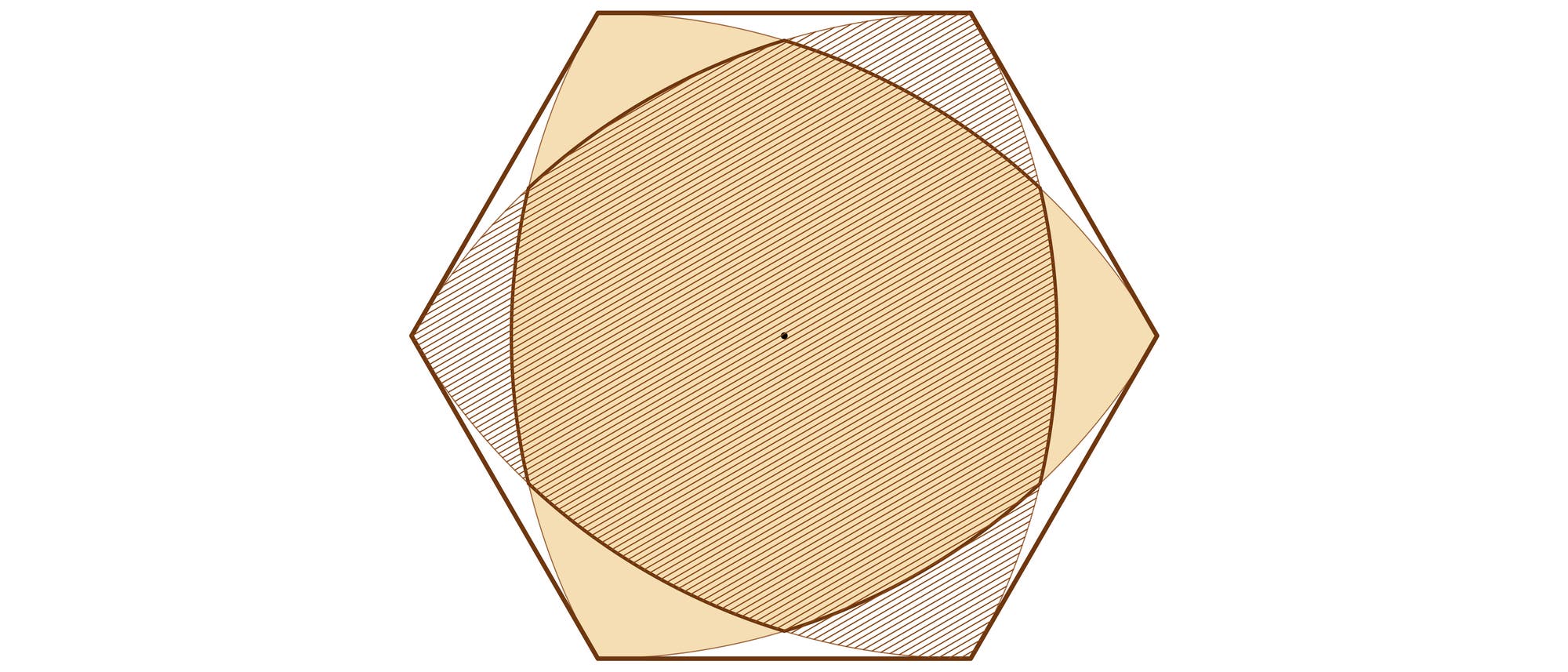
Der Satz von Kovner (auch als Satz von Kovner und Besicovitch zitiert) sagt: In jede konvexe ebene Figur kann man eine punktsymmetrische konvexe Figur zeichnen, deren Fläche mindestens 2/3 der ursprünglichen Figur beträgt. Für den Spezialfall des Dreiecks ist das leicht zu zeigen.
Punktsymmetrie ist beim Dreieck besonders bezüglich des Schwerpunktes interessant.
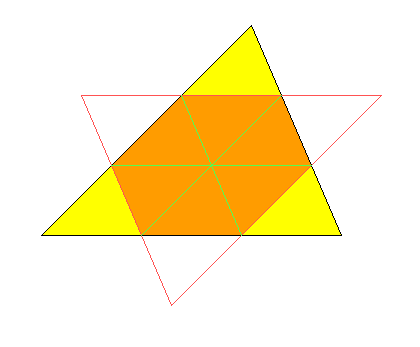
Spiegelt man das Dreieck an seinem Schwerpunkt und bildet die Schnittmenge aus dem so gewonnenen Bild und dem ursprünglichen Dreieck, so erhält man ein punktsymmetrisches Sechseck mit genau 2/3 der Fläche. Damit ist der Spezialfall des Satzes von Kovner für das Dreieck klar.
Natürlich kann man in das Dreieck auch kleinere punktsymmetrische Figuren zeichnen. Andererseits kann man auch Figuren finden, in die größere punktsymmetrische Figuren passen, am einfachsten solche, die selbst schon punktsymmetrisch sind wie Parallelogramme oder Kreise. Bei diesen ist die Fläche dann 100%.
Mehr dazu findet sich ab Seite 181 in Honsbergers "Footsteps".



Schreiben Sie uns!
Beitrag schreiben