Kreuzungsfreier Rundweg

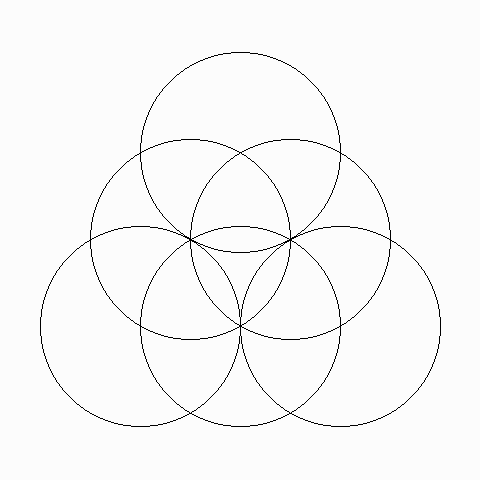
In einem botanischen Garten sind die Wege in Form von Kreisen angelegt. Es ist ziemlich leicht, einen Rundweg ("Rund"- Weg sozusagen in doppelter Bedeutung) zu zeichnen, der alle Wegstücke genau einmal durchläuft, warum eigentlich? Kann man auch einen Rundweg angeben, der an den Knotenpunkten ohne Kreuzung mit sich selbst auskommt?
T. H. O'Beirne hat zur Lösung solcher Probleme vorgeschlagen, die Flächen zu färben und dann zu umlaufen. Wir können hier sogar den gefärbten Teil weiter unterteilen:
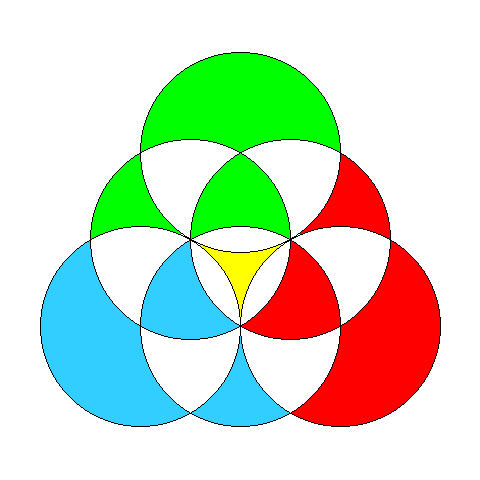
Dass das Problem überhaupt lösbar ist, ist eine Folge davon, dass jeder Knoten an einer geraden Anzahl von Wegstücken hängt (Euler-Graph).
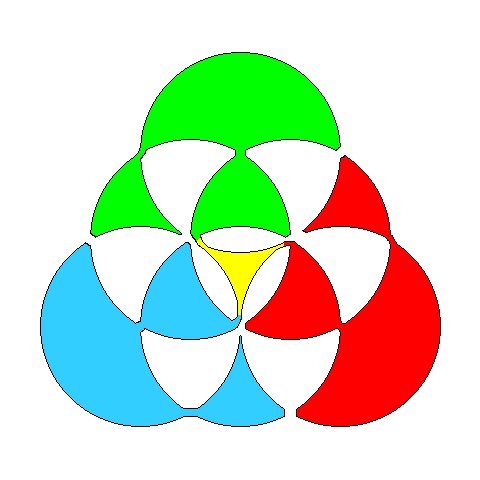
Jetzt ist es wesentlich leichter, einen kreuzungsfreien Weg zu suchen, der über alle Wegstücke genau einmal läuft:
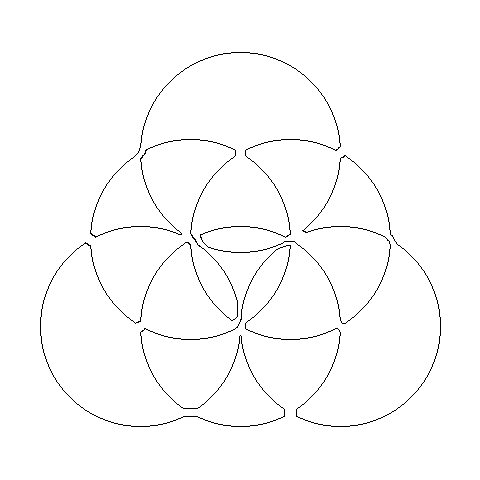



Schreiben Sie uns!
Beitrag schreiben