Hemmes mathematische Rätsel: Leiter und Kiste
Der englische Mathematiker Thomas Simpson wurde 1710 in Market Bosworth geboren und starb 1761 im Alter von nur fünfzig Jahren. Simpson war der Sohn eines einfachen Webers und arbeitete anfangs auch selbst als Weber. Nachdem er aber die Mathematik im Selbststudium erlernt hatte, arbeitete er als Mathematiklehrer in Nuneaton. 1733 musste er fliehen, weil er während einer Astrologiestunde als Teufel verkleidet ein Mädchen verängstigt hatte. Ab 1743 unterrichtete Simpson an der Royal Military Academy in London. Bekannt wurde er durch seine Arbeiten über die Interpolation und die numerische Integration und vor allem durch die nach ihm benannte Simpson-Regel. Er schrieb mehrere Bücher, darunter auch das 1745 in London erschienenen Werk »A Treatise of Algebra«. In diesem Buch stellte er seinen Lesern auf der Seite 250 eine Aufgabe, die für das heutige Rätsel mit einer anderen Einkleidung und mit anderen Zahlen versehen worden ist.
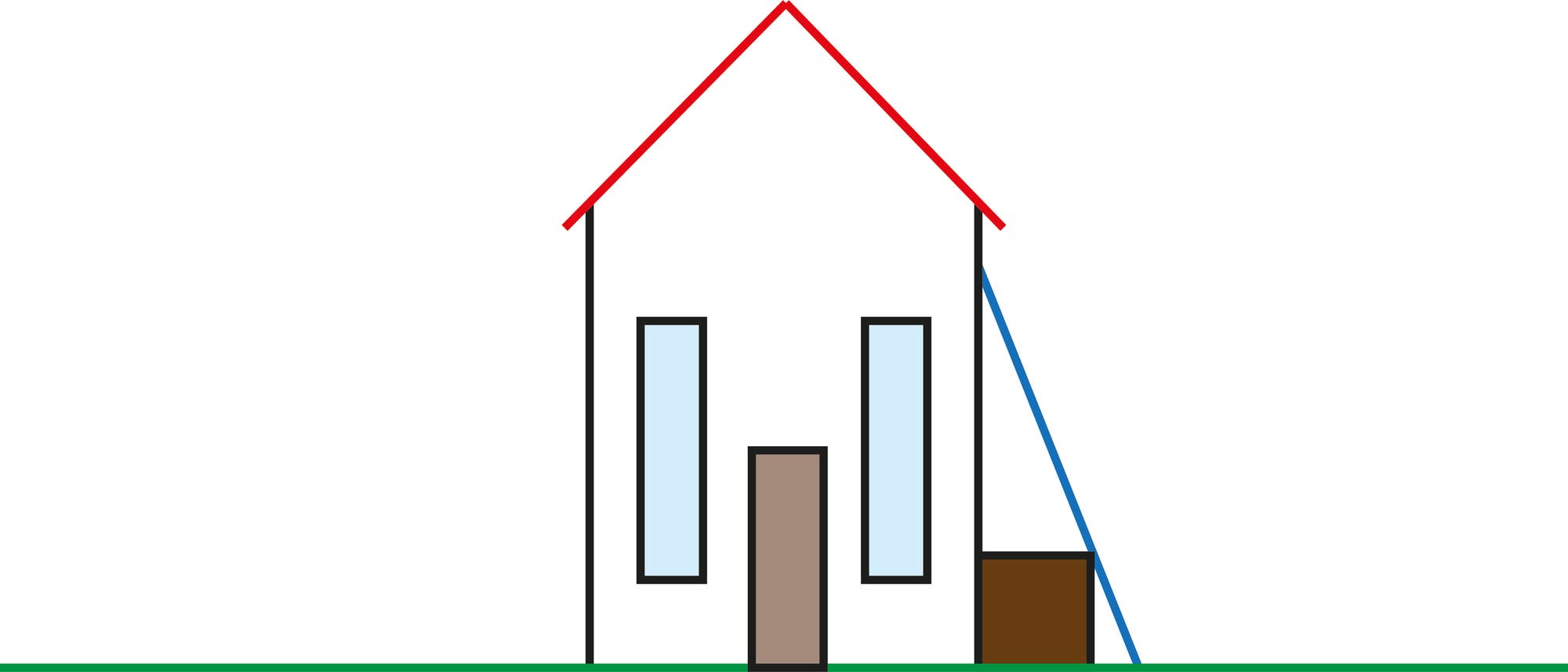
Eine große würfelförmige Kiste von 1,2 m Kantenlänge steht direkt an einer Hauswand auf dem Boden. Eine Leiter von 3,5 m Länge ist schräg an das Haus gestellt worden, so dass ihr Unterende auf dem Boden steht, ihr Oberende an der Wand lehnt, und sie zwischendurch auch noch eine Kante der Kiste berührt. In welcher Höhe über dem Boden trifft die Leiter auf die Hauswand?
Wir bezeichnen die Länge der Leiter mit L und die Kantenlänge der Kiste mit w. Die Leiter berührt in den Abständen x und y von der Unterkante des Hauses den Boden bzw. die Wand. Mit dem Satz des Pythagoras erhält man x2 + y2 = L2, was man zu (x + y)2 – 2xy = L2 umformen kann. Mit der Hilfsvariablen z = x + y wird daraus z2 – 2xy = L2.
Die beiden kleinen Dreiecke in der Skizze sind ähnlich. Darum gilt (x – w)/w = w/(y – w), was zu xy = wz vereinfacht werden kann. Das setzt man in die obige Beziehung ein und erhält dadurch z2 – 2wz = L2. Diese quadratische Gleichung hat als positive Lösung z = w + √(w2 + L2). Setzt man für die Würfelkante w und die Leiterlänge L die Werte 1,2 m und 3,5 m ein, erhält man z = 4,9 m.
Nun stellt man die Gleichungen xy = wz und z = x + y nach x um, setzt sie gleich und bekommt wz/y = z – y. Daraus ergibt sich die quadratische Gleichung y2 – zy + wz = 0, die zu den beiden Lösungen y1 = z/2 – √(z2/4 – wz) = 2,1 m und y2 = z/2 + √(z2/4 – wz) = 2,8 m führt. Die dazugehörigen x-Werte erhält man über die Gleichung x = z – y zu x1 = 2,8 m und x2 = 2,1 m. Die Leiter berührt also entweder 2,8 m oder 2,1 m über dem Boden die Hauswand.



Schreiben Sie uns!
Beitrag schreiben