Ein magisches Quadrat N-ter Ordnung ist ein quadratisches Raster mit N×N Unterquadraten, auf die die Zahlen von 1 bis N² so verteilt sind, dass die Summe der N Zahlen in jeder Zeile, in jeder Spalte und in den beiden Diagonalen jeweils gleich ist. Diese Summe bezeichnet man als die magische Konstante.

Das magische Quadrat 3. Ordnung ist das wohl bekannteste Quadrat. Es hat die magische Konstante 15 und war bereits im 4. Jahrhundert v. Chr. in China unter dem Namen Loh-Shu bekannt. Nach chinesischer Überlieferung soll es bereits um 2800 v. Chr. gefunden worden, was aber vermutlich nicht stimmt.

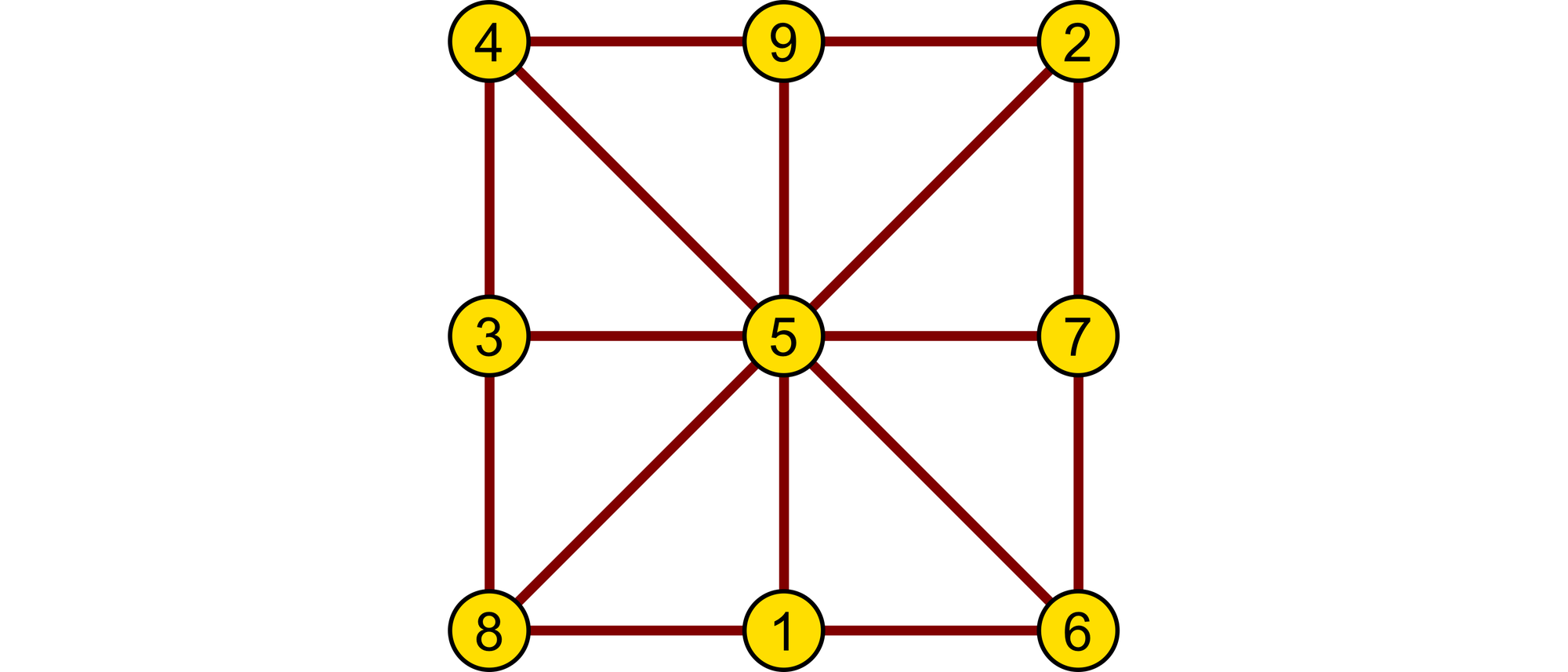
Der englische Elektroingenieur Lee Sallows lebt seit 1970 in Nimwegen in Niederlanden. Er ist ein weltweit anerkannter Experte für magische Figuren aller Art. Im September 2008 wandelte er das Loh-Shu etwas ab. Statt es durch ein Quadrat mit neun Unterquadraten darzustellen, deutete er es als Muster aus acht Strecken. Nun lautet die Aufgabe:

Wie muss man acht Strecken anordnen und darauf die Zahlen von 1 bis 9 verteilen, so dass auf jeder Strecke drei Zahlen stehen, die die Summe 15 ergeben? Die Lösung kann man mühelos aus dem Loh-Shu ableiten.

Dann fragte sich Lee Sallows: Kann man die acht Strecken und die Zahlen von 1 bis 9 auch so anordnen, dass die magische Konstante nicht 15 ist? Natürlich müssen trotzdem auf jeder Strecke drei Zahlen stehen.