Parallelogramm

Wenn in einem ebenen Viereck zwei einander gegenüberliegende Seiten gleich lang und zwei einander gegenüberliegende Winkel gleich sind, handelt es sich um ein Parallelogramm. Stimmt das immer?
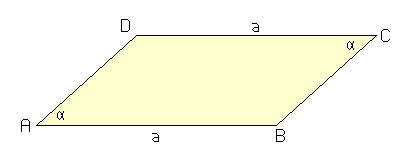
Versuchen Sie ein Gegenbeispiel zu finden!
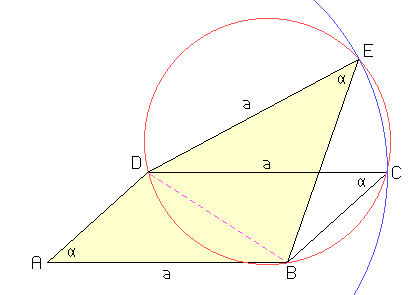
Wir behalten die Ecken \(A\), \(B\) und \(C\) und schlagen einen (hier blau gezeichneten) Kreis um \(D\) mit dem Radius \(a = AB = CD\). Alle Punkte auf ihm haben von \(D\) die Entfernung \(a\).
Dann zeichnen wir den (roten) Kreis durch \(B\), \(C\) und \(D\). Wir unterscheiden von diesem Kreis zwei Teile (Bögen), die durch \(B\) und \(D\) voneinander getrennt sind; auf einem von ihnen liegt \(C\). Alle Punkt auf diesem Teil "sehen" die Diagonale \(BD\) unter dem gleichen Winkel \(\alpha\) (Sehnen-Winkel-Satz, auch als Satz vom Umfangswinkel bekannt). Die Punkte auf dem anderen Teil des Kreises sehen BD dagegen unter dem Winkel \(\pi-\alpha\).
Der rote und der blaue Kreis haben auf jeden Fall den Punkt \(C\) gemeinsam, und wenn sie sich dort nicht gerade berühren (d. h. eine gemeinsame Tangente haben), dann haben sie noch einen zweiten Schnittpunkt \(E\). Wenn dieser auf dem gleichen Teil des roten Kreises liegt wie \(C\), so erfüllt das Viereck die Bedingung, dass zwei Gegenseiten gleich lang sind, nämlich \(AB\) und \(ED\), und dass zwei einander gegenüberliegende Winkel (das Wort "Gegenwinkel" hat eine speziellere Bedeutung!) ebenfalls gleich sind, nämlich \(\angle DAB\) und \(\angle DEB\). Das Viereck \(ABED\) ist aber keineswegs ein Parallelogramm, nicht einmal ein Trapez.
Dass man einen Satz ("Im Parallelogramm sind ...") nicht einfach umkehren kann ("Wenn ..., dann ist es ein Parallelogramm") sollte ja klar sein, dass es aber in diesem Fall ernst damit ist, überrascht schon so Manchen (damit möchte ich dezent andeuten, dass ich auch darauf hereingefallen bin).
Dabei ist das Ganze nur eine etwas versteckte Anwendung des Kongruenzsatzes "SsW": Wenn zwei Dreiecke (bei uns \(BCD\) und \(BED\)) zwei Seiten und einen nicht zwischen ihnen liegenden Winkel gemeinsam haben, dann müssen sie nur dann deckungsgleich sein, wenn der fragliche Winkel der größeren der beiden Seiten gegenüberliegt.



Schreiben Sie uns!
Beitrag schreiben