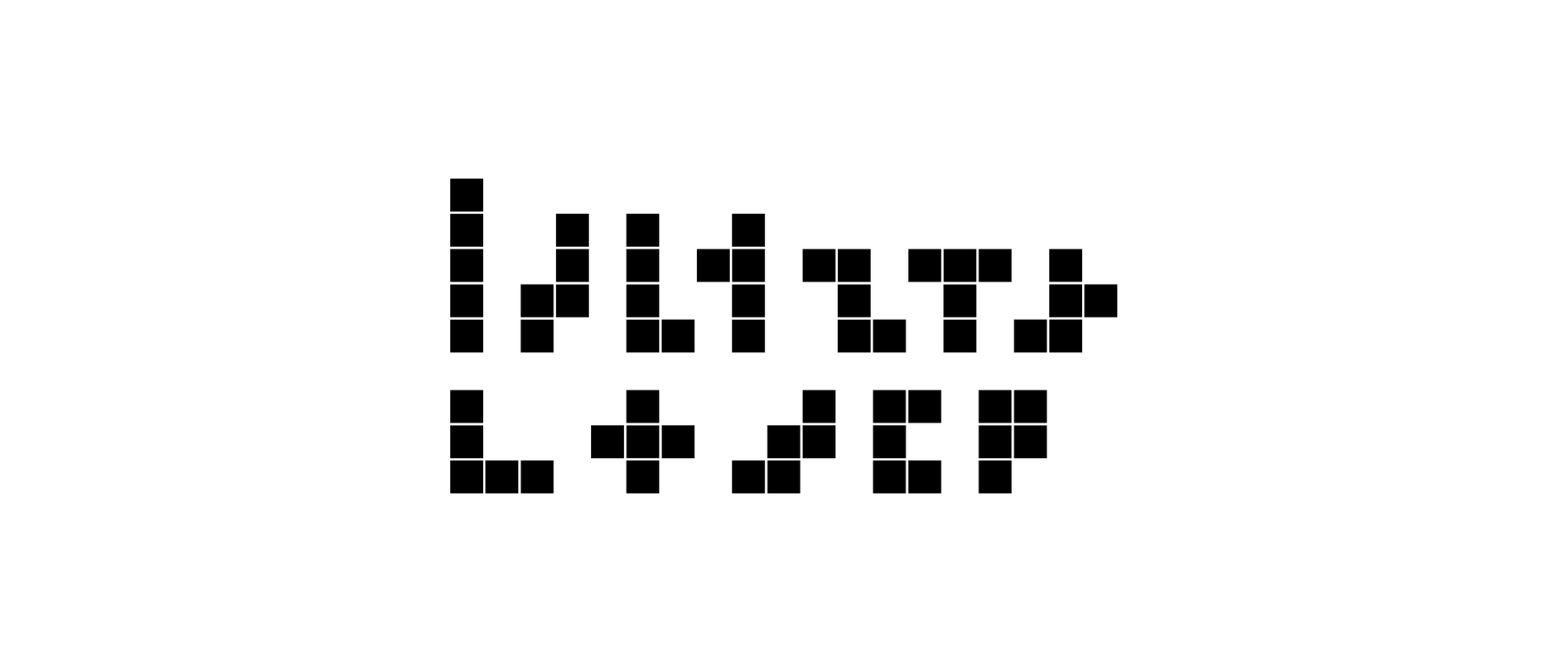
Der englische Chemiker Thomas Rayner Dawson wurde 1889 in Leeds geboren. Er war Vizepräsident des britischen Instituts der Kautschukindustrie. In seiner Freizeit erfand er Schachprobleme, die er in vielen Zeitschriftenartikeln und elf Büchern veröffentlichte. Dawson war von 1930 bis kurz vor seinem Tod 1951 Herausgeber der Fairy Chess Review. In dieser Zeitschrift veröffentlichten er und andere Autoren zahlreiche Probleme mit geometrischen Figuren, die aus lauter Quadraten bestanden. Eine besondere Gruppe dieser Figuren waren die Pentominos. Sie bestehen aus jeweils fünf gleichen Quadraten, die an den Kanten miteinander verbunden sind. Es gibt insgesamt zwölf verschiedene Pentominos, wobei gedrehte und gespiegelte Figuren als gleich gezählt werden.

Legen Sie zwei der zwölf Pentominos so auf ein 5×5-feldiges Spielfeld, dass keines der zehn anderen Pentominos mehr darauf Platz findet. Dabei dürfen die Steine umgeklappt werden, sodass die Vorder- zur Rückseite wird. Die Quadrate der Pentominos und des Spielfeldes sind gleich groß, und die Steine müssen so auf das Brett gelegt werden, dass die Quadrate genau aufeinander fallen. Außerdem darf keine Pentomino über den Rand des Spielfeldes ragen. Mit welchen beiden Pentominos lässt sich die Aufgabe lösen?