Hemmes mathematische Rätsel: Plumpudding Castle
Der russisch-amerikanische Mathematiker Alexander Soifer wurde 1948 in Moskau geboren und studierte an der Staatlichen Pädagogischen Universität Moskau. Seit 1979 ist er Professor für Mathematik an der University of Colorado. Er war 1996 bis 2005 im amerikanischen Komitee der Internationalen Mathematikolympiade. Seit 1996 ist er Sekretär der »World Federation of National Mathematics Competitions« (WFNMC) und seit 2008 deren Senior Vice President. Alexander Soifer hat eine ganze Reihe Bücher mit unterhaltsamen Mathematikproblemen geschrieben, von denen leider bisher keines auf Deutsch erschienen ist. 1983 gründete er seinen eigenen Mathematikwettbewerb für Schüler, die »Colorado Mathematical Olympiad«, der am 17. April 1987 zum vierten Mal stattfand. In dieser Runde wurde den Teilnehmern eine Aufgabe gestellt, die Mikhael Serov erdacht hatte. Sie ist für »Spektrum.de« leicht verändert worden.
Plumpudding Castle, eine der merkwürdigsten Burgen Schottlands, hat einen dreieckigen Grundriss und ausschließlich dreieckige Räume, die gleich geformt sind. Alle benachbarten Räume sind durch Türen miteinander verbunden. Das Burggespenst geistert jede Nacht durch das alte Gemäuer. Dabei betritt es in keiner Nacht einen Raum zweimal, und es verlässt die Burg niemals. Angenommen, Plumpudding Castle hat 100 Räume, wie viele kann das Gespenst in einer Nacht höchstens betreten?
Die 100 dreieckigen Räume der dreieckigen Burg lassen sich schachbrettartig rot und gelb färben, so dass zwei benachbarte Räume immer unterschiedlich gefärbt sind. Das Gespenst betritt also auf seiner nächtlichen Tour immer abwechselnd einen roten und einen gelben Raum.
Der Grundriss der Burg hat in der obersten Reihe ein rotes Dreieck, in der zweiten Reihe zwei rote Dreiecke, in der dritten drei rote Dreiecke usw. Insgesamt enthält er 1 + 2 + 3 + ... + 10 = 55 rote Dreiecke. Von den gelben Dreiecken gibt es in jeder Reihe eines weniger als rote Dreiecke, also insgesamt nur 0 + 1 + 2 + ... + 9 = 45.
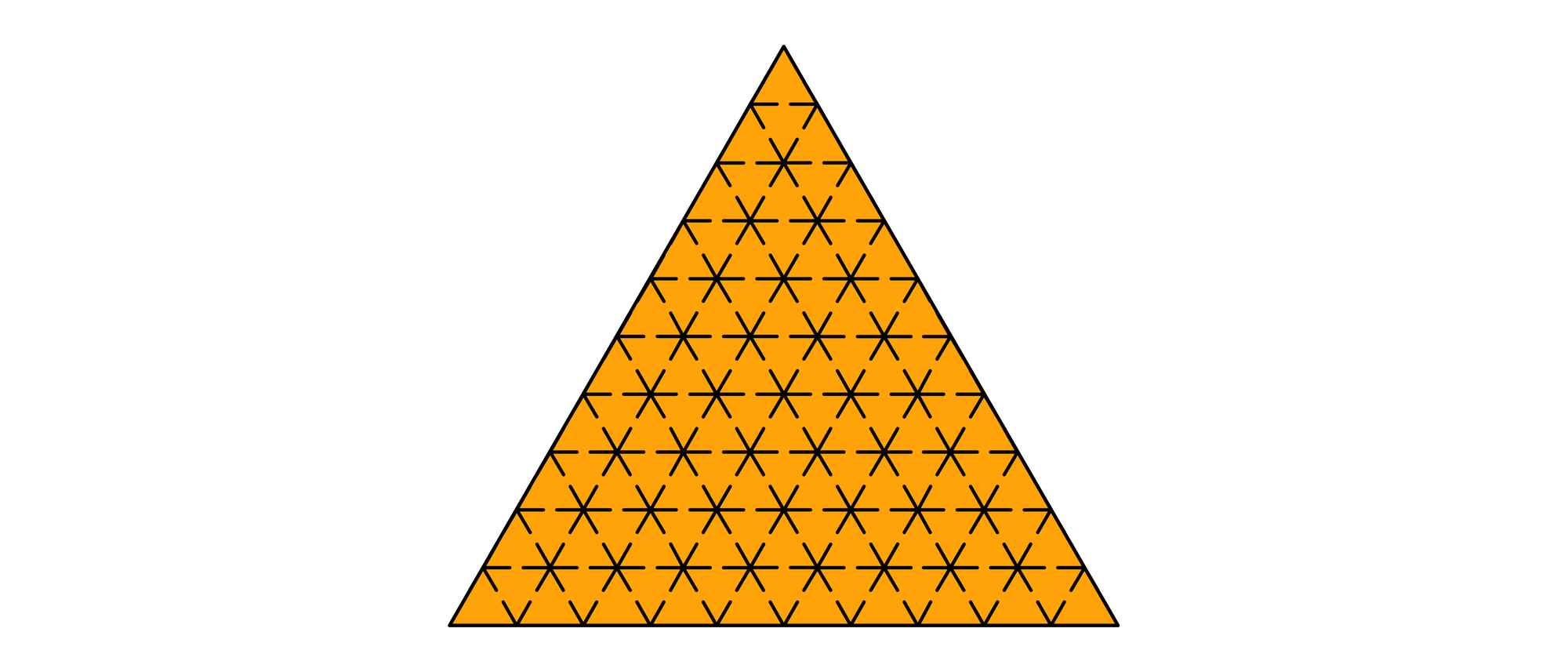
Da das Gespenst nach jedem roten Raum in einen gelben Raum gehen muss, kann es, wenn es seine Wanderung in einem roten Raum beginnt, höchstens 45 gelbe und 46 rote Räume betreten, also insgesamt 91 Räume. Dass das Gespenst auch tatsächlich 91 Räume erreichen kann, oder anders formuliert, dass es nur 9 Räume nicht erreichen kann, zeigt die Skizze. In jeder Reihe, außer in der obersten, betritt das Gespenst einen Raum nicht.



Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.