Hemmes mathematische Rätsel: Punkte in bunten Dreiecken
Der 1944 geborene Schweizer Mathematiker Hans Walser hat viele Jahrzehnte lang als Lehrer an Gymnasien und als Lehrbeauftragter an Universitäten unterrichtet. Er hat eine große Zahl von Aufsätzen für Fachzeitschriften und auch etwa ein Dutzend Bücher verfasst. Sein neuestes Werk heißt »EAGLE-Malbuch: Formen und Farben« und ist ein Malbuch mit geometrischen Formen für Erwachsene. Es ist 2015 in der Edition am Gutenbergplatz in Leipzig erschienen. Walser hat auch eine große Zahl mathematischer Miniaturen geschrieben und aufwendig grafisch gestaltet, die man im Internet finden kann. Das heutige Rätsel stammt aus einer seiner Miniaturen.
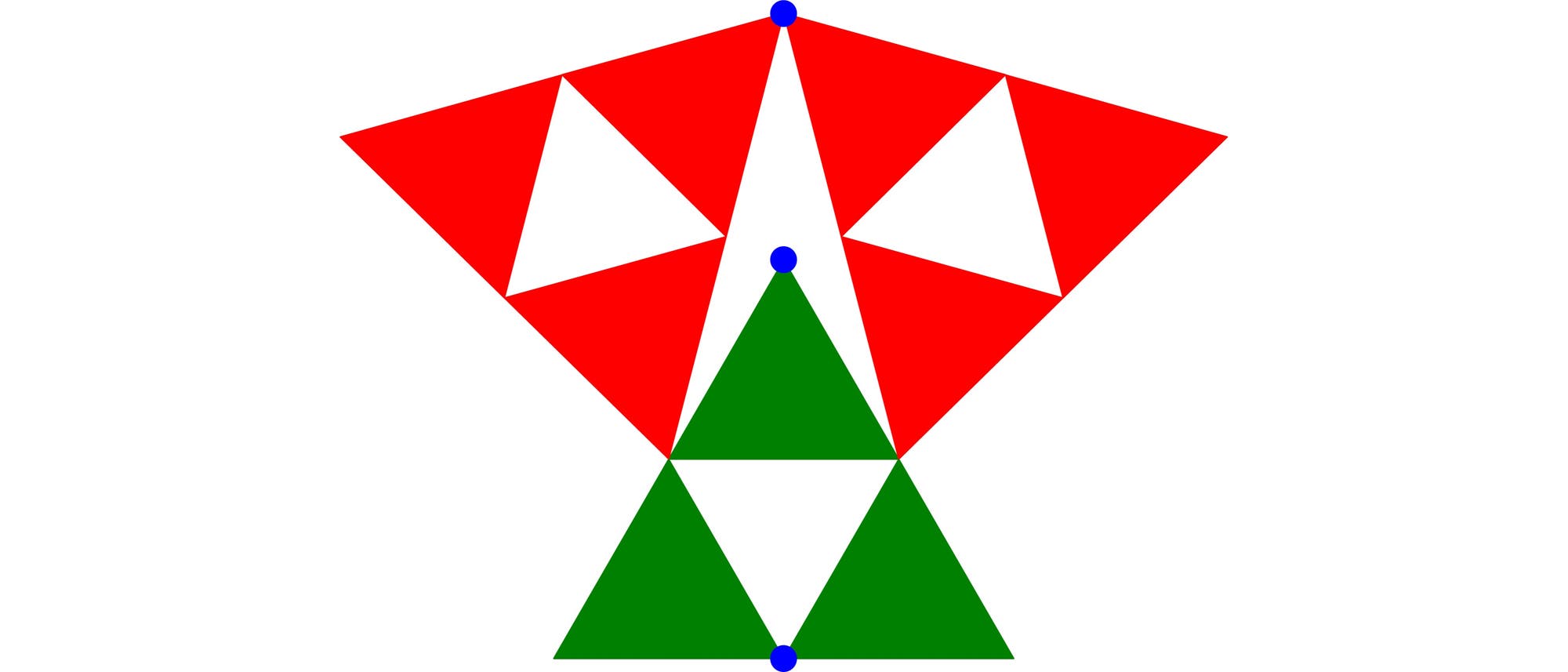
Alle roten und grünen Dreiecke sind gleichseitig und gleich groß und die drei blauen Eckpunkte liegen genau übereinander. In welchem Verhältnis steht der Abstand der beiden unteren blauen Punkte zum Abstand der beiden oberen blauen Punkte?
Nehmen wir einmal an, alle roten und grünen Dreiecke haben die Seitenlänge 2. Die Linie zwischen dem mittleren blauen und dem gelben Punkt ist die Höhe h des oberen grünen Dreiecks und kann mit dem Satz des Pythagoras zu h = √(22 – 12) = √3 berechnet werden.
Der Abstand der beiden unteren blauen Punkte beträgt folglich a = 2h = 2 • √3. Auch den Abstand g des oberen blauen vom gelben Punkt erhält man mit Satz des Pythagoras, und es gilt g = √(42 – 12) = √(15) = √5 • √3. Somit ist der Abstand der beiden oberen Punkte b = g – h = √5 • √3 – √3 = (√5 – 1) • √3.
Das gesuchte Verhältnis beträgt darum a/b = 2 • √3 / ((√5 – 1) • √3) = 2 / (√5 – 1) = (√5 + 1) / 2 ≈ 1,618. Dieses Verhältnis ist der berühmte goldene Schnitt, ein Streckenverhältnis, das seit der Antike in der Kunst und in der Architektur verwendet und als besonders ästhetisch empfunden wird.
Schreiben Sie uns!
Beitrag schreiben