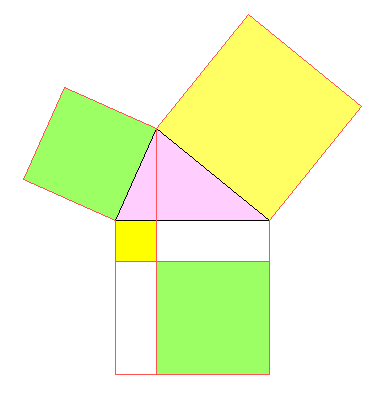
Wir wenden zweimal den Satz von Pythagoras auf die eingezeichnete Höhe an und finden einerseits \(b^2=h^2+p^2\)

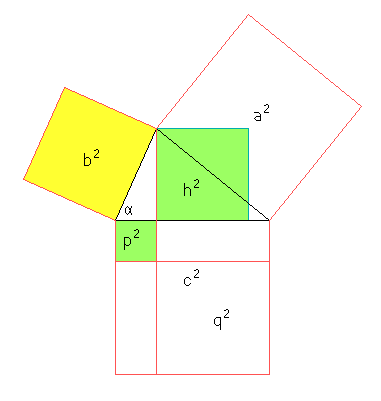
und andererseits \(a^2=h^2+q^2\):

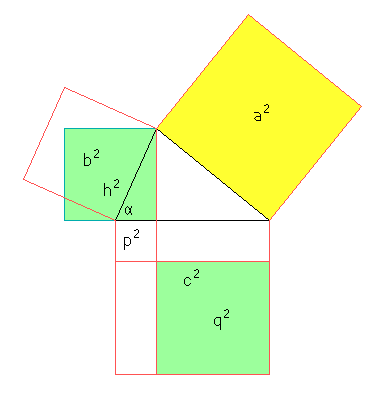
Werfen wir \(h^2\) aus beiden Gleichungen heraus ("eliminieren" klingt etwas vornehmer), so gibt es unsere Behauptung \(a^2+p^2=b^2+q^2\):

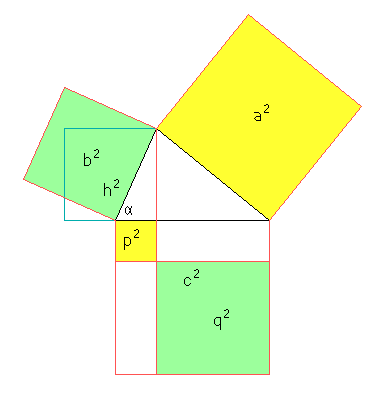
Wegen \(c = p + q\) ist daher \(a^2=b^2+c^2-2cp\). Im Bild bedeutet das, dass man \(c \cdot p\) nicht einfach zweimal abziehen kann, sondern die Überlappung \(p^2\) wieder einmal nachfüllen muss, damit es wieder stimmt.

Wegen der goniometrischen Bezeichnung von \(p\) als \(b \cos(\alpha)\) nennt man den Satz den Cosinus-Satz (der ebenen Trigonometrie, im Gegensatz zu den Cosnius-Sätzen der Kugel, wo es gleich deren zwei gibt) und schreibt ihn \[a^2=b^2+c^2-2bc \cos(\alpha) \; .\]

Da in unserem Dreieck alle Ecken und alle Winkel gleichberechtigt sind, gilt die Formel auch mit zyklischer Vertauschung der Winkel- und Seiten-Bezeichnungen.

Man kann den Cosinus-Satz auch durch Ausschreiben von \(h = b \sin(\alpha)\), \(q = c – b \cos(\alpha)\) und (was wir ja auch gemacht haben:) \(p = b \cos(\alpha) \) herleiten.