Hemmes mathematische Rätsel: Quadrate im Rechteck
Das populärwissenschaftliche britische Magazin »New Scientist« erscheint seit 1956 jede Woche. Seit dem 22. Februar 1979 findet man darin eine Denksportkolumne mit dem Titel »Enigma«, die einige Jahre lang von Eric Emmet, Martin Hollis und Stephen Ainley geschrieben wurde. Die Kolumne lief fast 35 Jahre lang, wenn auch die Autoren mehrfach wechselten. Am 28. Dezember 2013 erschien das 1780. und letzte »Enigma«. Am 14. Juni 1979 stellte Stephen Ainley, der zwischen 1937 und 1940 in Cambridge studierte und sich selbst als frustrierten Mathematiker bezeichnete, als Enigma Nr. 17 folgende Aufgabe:
Das kleinstmögliche Rechteck, in das man die Quadrate mit den Seitenlängen 1, 2, 3 und 4 setzen kann, ohne dass sie sich überlappen oder über den Rand des Rechtecks ragen, hat die Größe 7×5. Dabei bleibt eine Fläche von fünf Quadrateinheiten unbedeckt.
Wie groß ist die unbedeckte Fläche beim kleinsten Rechteck, in das man alle Quadrate mit den Seitenlängen von 1 bis 8 unterbringen kann? Die Seiten der Quadrate dürfen nur parallel oder senkrecht zu den Seiten des Rechtecks liegen.
Ich habe die Aufgabe etwas vereinfacht. Im Original müssen mehr als acht Quadrate in das Rechteck gepackt werden.
Alleine um die beiden größten Quadrate mit den Seitenlängen 7 und 8 in einem Rechteck unterzubringen, muss dessen kurze Seite mindestens 8 und dessen lange mindestens 15 Einheiten lang sein. Da die acht Quadrate eine Gesamtfläche von 12 + 22 + 32 + 42 + 52 + 62 + 72 + 82 = 204 Quadrateinheiten haben.
Nur das 17×24-Rechteck hat eine Fläche von 204 Quadrateinheiten und erfüllt die beiden Seitenlängenbedingungen. Allerdings lassen sich in ihm, wie man leicht überprüfen kann, nicht alle acht Quadrate unterbringen.
Die nächst größeren Rechtecke, die die beiden Seitenlängenbedingungen erfüllen, sind 23×9 = 207, 16×13 = 208, 26×8 = 208, 19×11 = 209, 21×10 = 210 und 15×14 = 210. Durch systematisches Probieren stellt man schnell fest, dass die acht Quadrate in keines der Rechtecke der Flächen 207 bis 209 passen.
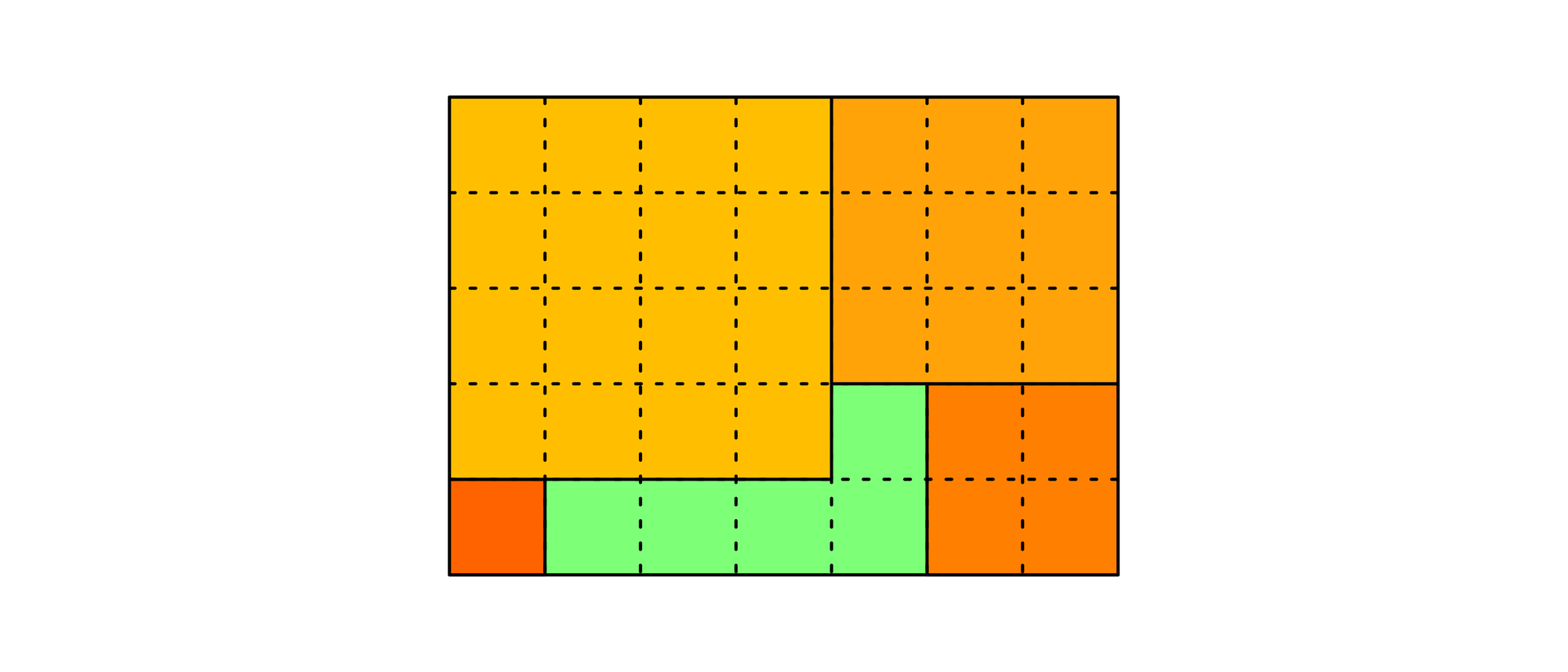
Erst das zweite der 210 Quadrateinheiten großen Rechtecke kann sie alle aufnehmen. Dabei bleiben sechs Quadrateinheiten unbedeckt.
Es gibt mehrere Möglichkeiten, wie die acht Quadrate in dem Rechteck angeordnet werden können. Das Bild zeigt eine davon.



Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.