Rauten
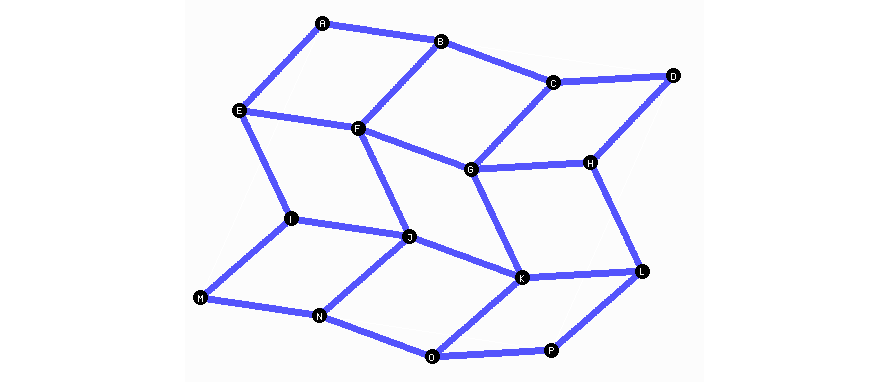
Charly hat aus gleichlangen Stangen ein Gitter mit 3 mal 3 Quadraten zusammengeschraubt. Leider hat er die Schrauben nicht gegen Drehen gesichert, und so hat er nun ein ebenes Netz aus Rauten.
Was kann man über die vier äußeren Ecken sagen?
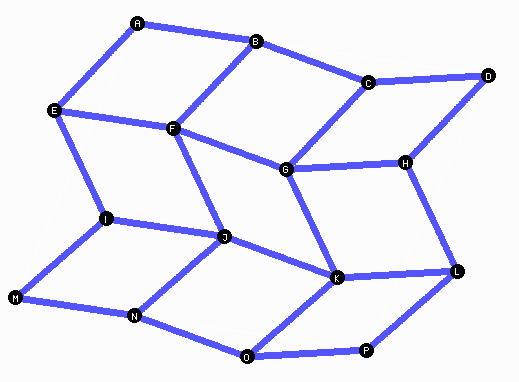
Betrachten Sie Ketten wie \(EFGH\) und ähnliche. Wenn Sie einen Metallbaukasten haben, oder 24 Lochstreifen aus dem Büro und 16 Klammern zum Verschließen von Briefen oder – noch besser – eine Ösenzange und 16 Ösen, können Sie das sehr schön nachspielen.
Das Wort "ähnlich" im Tipp ist ganz wörtlich gemeint: Die Ketten \(ABCD\), \(EFGH\), \(IJKL\) und \(MNOP\) sind zueinander ähnlich (sogar kongruent) und gegeneinander parallelverschoben. Sie haben also insbesondere auch gleiche Abstände zwischen ihren Enden wie \(AD\) und \(MP\). Das Gleiche gilt für die "vertikalen" Ketten \(AEIM\) und so weiter. Die äußeren Ecken \(ADPM\) bilden daher ein Parallelogramm.
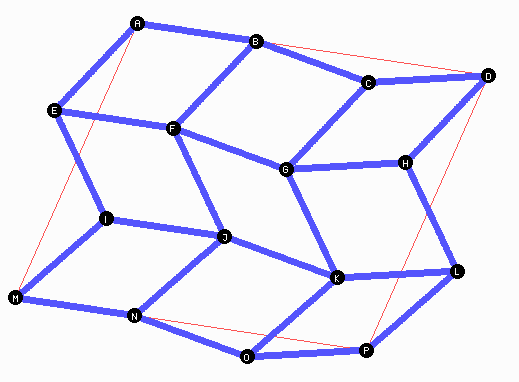
Nun verlangen wir, dass vier "diagonale" Punkte, also entweder \(A F K P\) oder \(D G J M\) auf einer Geraden liegen sollen. Dabei dürfen die Abstände von einem Punkt zum nächsten durchaus ungleich sein.
Das Parallelogramm wird dann zu einer Raute, und die erwähnte Gerade wird zur Symmetrieachse auch für die ganze Figur mit allen Einzelheiten.
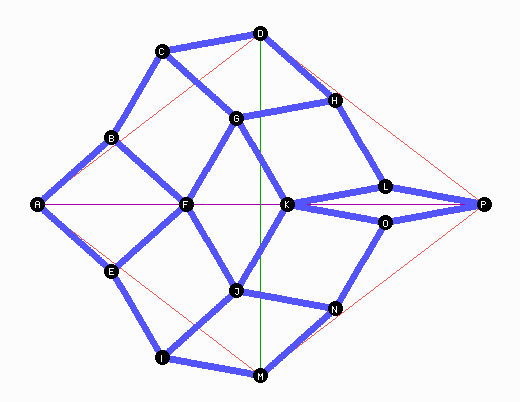
Aber wieso?
Im unteren Bild sind gleich gefärbte Stangen parallel zueinander oder liegen bezüglich der horizontalen Achse spiegelbildlich zueinander. Damit liegen \(D\) und \(M\) gleich weit von der Achse \(AP\) entfernt.
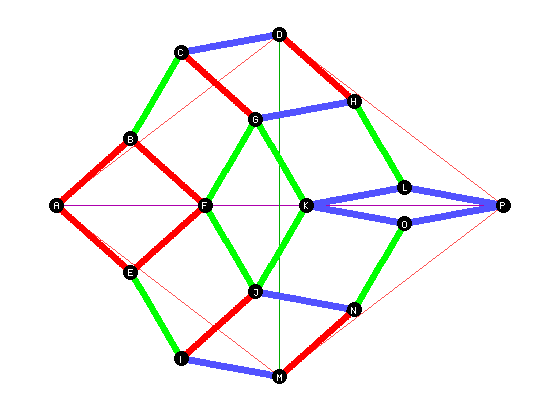
Die beiden langen waagerechten Stangen (Bild unten) bilden zwischen sich eine ebenso lange Schiene, in der die herausschauenden Schrauben geführt werden. Die Symmetrie zu ihr als waagerechter Achse ist zwangsläufig.


Diese Teilaufgabe geht durch geringfügige Verallgemeinerung aus dem Problem der gestapelten Rohre hervor, deren Achsen etwas weniger Freiheit haben.
Es ist wohl klar, dass es mit 4 mal 4 oder 5 mal 5 (usw.) Rauten genau so geht.



Schreiben Sie uns!
Beitrag schreiben