Überlegen Sie sich dazu folgendes Beispiel:

In einer Klasse aus 27 Personen wird ein Hochsprung-Wettbewerb gemacht. Der Lehrer, der ein Herz für die Benachteiligten hat, schickt nun das schlechteste Drittel für ein Wochenende in ein Trainingslager und ist vom Erfolg begeistert, denn die Ergebnisse beim Wiederholungstest sind deutlich besser! Daraufhin schlägt der Schulleiter vor, auch das beste Drittel zum Training zu schicken, damit die Schule beim nächsten Sportfest mehr Medaillen bekommt. Leider ist das Ergebnis eine große Enttäuschung: Der zweite Test fällt deutlich schlechter aus als der erste. Was ist vom Trainingslager zu halten?

Der Mathe-Lehrer schlägt als Annahme vor, dass das Training wirkungslos ist und dass von den 27 Teilnehmer(inne)n je neun lange (A), mittellange (B) und kurze Beine (C) haben und im persönlichen Mittelwert entsprechend hoch oder nicht so hoch springen können. Außerdem habe jeweils ein Drittel jeder Gruppe beim ersten Test – beziehungsweise beim zweiten – einen guten oder einen schlechten oder einen neutralen Tag gehabt.

Das Bild unten zeigt die Leistungen der Schüler an den beiden Testtagen. Die roten Linien grenzen ab, wer beim ersten oder zweiten Test zum besten beziehungsweise zum schlechtesten Drittel gehört hat. Man sieht ohne Nachrechnen, dass die Schüler, die beim ersten Test am besten abschnitten, beim zweiten Test deutlich näher beim Durchschnitt lagen – aber umgekehrt genau so: Die Gruppe, die beim zweiten Test das beste Drittel bildete, war im Schnitt beim ersten Test nicht so gut.

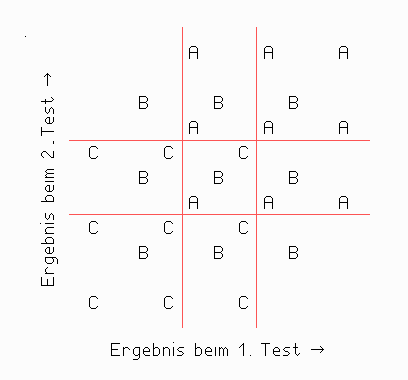
Wenn man also fragt, wie gut die Gewinner des zweiten Tests beim ersten waren, kommt man zum Ergebnis, dass sie sich zwischendurch verbessert haben (und die Verlierer in diesem Sinne verschlechtert). Wer aber vom ersten Test ausgeht, stellt fest, dass sich die Gewinner scheinbar verschlechtert und die Verlierer verbessert haben. In Wirklichkeit ist aber überhaupt nichts passiert, man hat nur zwei verschiedene Stichproben genommen, ohne sich über die Folgen klar zu sein.

In beiden Tests sind die zufälligen Effekte unabhängig voneinander, und die zeitliche Reihenfolge spielt keine Rolle. Wenn man eine Stichprobe wählt, die bei einem der Tests extrem ist, so ist diese es beim anderen nicht in gleichem Maße.

Im Beispiel der Sportgruppe gibt es zwei Extremfälle:

• Wenn die Beine aller Schüler gleich lang sind, hängt sozusagen alles von der Tagesform und damit gewissermaßen nur vom Zufall ab. Die Gruppe, die beim einen Test Sieger (oder Verlierer) ist, entpuppt sich beim anderen als genau durchschnittlich.
• Im anderen Extremfall spielt die Tagesform gar keine Rolle, sondern nur die Länge der Beine. Dann bleiben die Guten so gut wie zuvor und die anderen entsprechend. Alle Punkte im Diagramm liegen dann auf einer diagonalen Geraden. Wenn man aus einer Punktwolke mit Mischung aus Zufall und Systematik eine solche Gerade – mit Augenmaß oder mit stochastischen Methoden – herauspräpariert, so wird diese aus historischen Gründen "Regressionsgerade" genannt. Paradox ist diese Benennung: Die Punktwolke verwandelt sich genau dann in die Regressionsgerade, wenn der als Regression missdeutete Scheineffekt gar nicht auftritt.

Dieser Effekt taucht häufig auf: Wer rückblickend die erfolgreichen Teilnehmer einer Fortbildung betrachtet, findet eine Verbesserung; wer die vorher besseren auswählt, ist vom Erfolg der Fortbildung enttäuscht. Das ist vergleichbar mit einem perspektivischen Deutungsfehler: Wenn man durch zwei zueinander parallele offene Türen blickt, kann man durch die nähere Tür die andere ganz und noch ein Stück Wand rundherum sehen, umgekehrt aber auch. Ein Schluss auf ungleiche Größen der Türen wäre also sehr unsicher.

Ebenso haben also auch die überdurchschnittlich großen Kinder Eltern, die weniger über den Durchschnitt ragen, und das würde ein Biologe bestimmt nicht "Regression" nennen (sondern vielleicht "Supergression"). Die Regressions-Täuschung führt zu ernsthaften Fehldeutungen von gut gemeinten Maßnahmen, offenbar nicht nur bei Laien.

Kein Geringerer als Sir Francis Galton fand den vermeintlichen "Effekt" bei den Körpergrößen von Vätern und Söhnen und auch die Bezeichnung "Regression", weil er darin einen Trend der Natur zum Mittelmaß zu erkennen glaubte.