Satz von Raffael
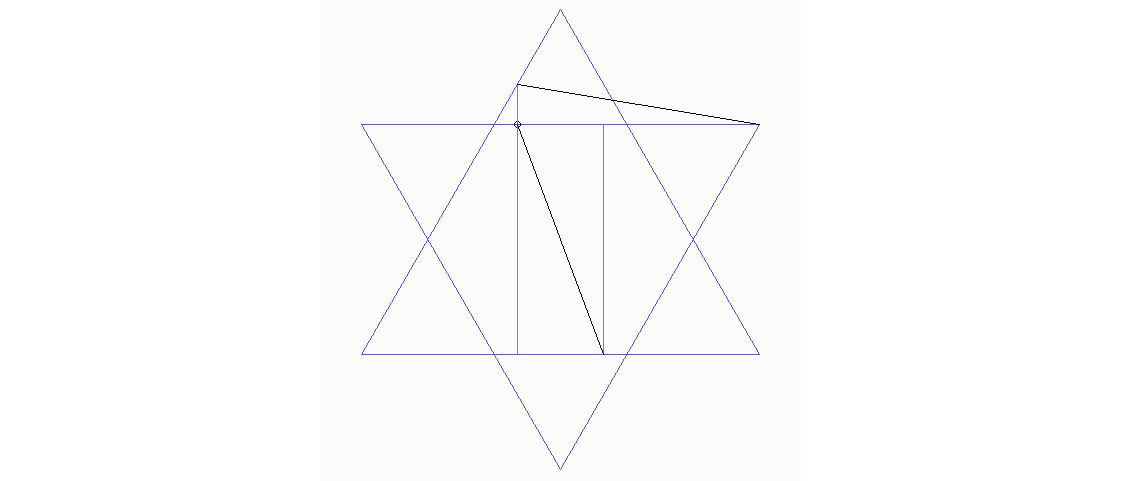
In dem Bild "Schule von Athen" von Raffaello Santi (dem auch Dresden und der Rest der Welt die sixtinische Madonna verdanken) sieht man eine geometrische Figur am Boden: ein Hexagramm mit zwei Parallelen darin. Nach dem Wissenschaftshistoriker John Lewis Heilbron gehört dazu ein Satz, der möglicherweise von Raffael selbst gefunden wurde. Er besagt, dass in dieser Zeichnung die beiden schwarzen Strecken gleich lang sind, wenn die roten Parallelen symmetrisch zur Symmetrieachse des Hexagramms wandern. Finden Sie einen Beweis dazu?
Da die Zacken des Hexagramms aus gleichseitigen Dreiecken mit Kantenlänge \(a\) bestehen, ist das pinke Dreieck ein "halbes gleichseitiges Dreieck": Seine kürzeste Seite \(b\) ist stets halb so lang wie die längste.
Das untere gelbe rechtwinklige Dreieck besitzt auf Grund der Symmetrie bezüglich der Achse des Hexagramms eine waagerechte Seite der Länge \(a-2b\). Das obere gelbe Dreieck hat auf dem Zacken ebenfalls eine Seite der Länge \(a-2b\). Zudem sind auch die langen Katheten der beiden gelben Dreiecke gleich lang, und zwar ist die gemeinsame Länge sowohl gleich dem Abstand zweier Spitzen des Hexagramms (blau) als auch der Länge der roten Parallelen. Also sind beide gelben Dreiecke deckungsgleich und daher auch die zwei schwarzen Strecken gleich lang.
Man kann die Parallelen auch noch weiter wandern lassen, so dass sich die gelben Dreiecke überlappen.
Die Animation zeigt aus naheliegenden Gründen nur Rechtecke, die ganz im Inneren des einbeschriebenen Sechsecks aus dem Hexagramm liegen. Roland Schröder stellt ergänzend fest, dass der Satz auch dann noch gilt, wenn das Rechteck größer ist, als in der Animation dargestellt.
Gefunden bei Heilbron, dort mit einem ziemlich umständlichen Beweis.
Schreiben Sie uns!
Beitrag schreiben