Hemmes mathematische Rätsel: Schwerter und Scheiden
Der Mathematiker Ulrich Graf wurde 1908 in Wolgast in Vorpommern geboren und starb 1954 in Düsseldorf. Er studierte Mathematik, Physik und Philosophie und erhielt 1938 eine Professur an der Technischen Hochschule in Danzig. Nach dem Krieg musste er Danzig verlassen und arbeitete an verschiedenen Universitäten in Westdeutschland, wo er die mathematische Statistik zu seinem Hauptarbeitsgebiet machte. Bekannt wurde er vor allem durch sein Buch über darstellende Geometrie, das er bereits 1937 veröffentlichte und das zu einem Standardlehrbuch wurde. Bis 1991 erschien es in insgesamt zwölf Auflagen.
Ulrich Graf hat aber auch ein Buch über Unterhaltungsmathematik geschrieben, das 1942 in Dresden erschien. Es hat den Titel »Kabarett der Mathematik« und enthält mathematische Kuriositäten, Spielereien und Rätsel, aber auch Gedichte und Aphorismen über Mathematik. Aus diesem Buch stammt das folgende Problem:
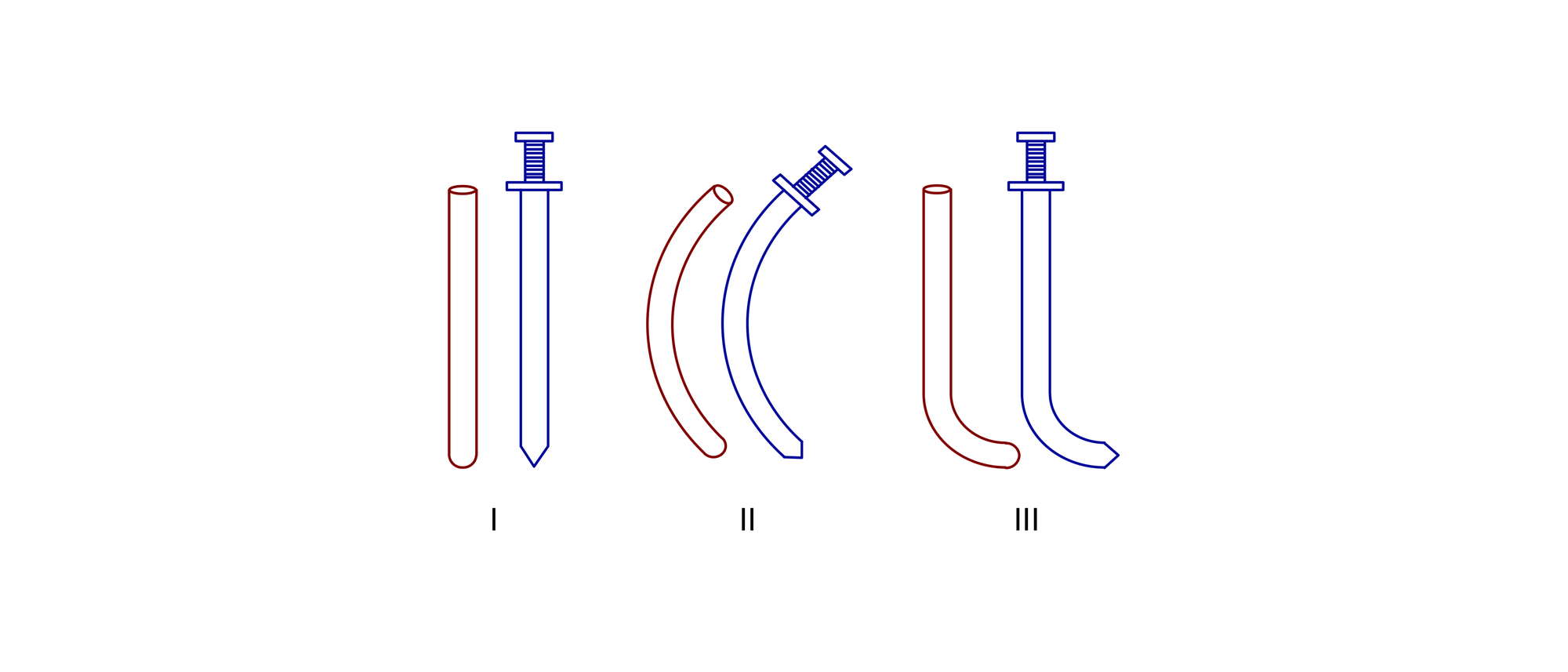
Nur ein Schwert mit einer gleichmäßigen Krümmung lässt sich in eine eng anliegende Scheide stecken. Zwei bekannte Kurven, die diese Eigenschaft besitzen, sind die Strecke und der Kreisbogen. Beide Formen sind auch als Waffen verwirklicht: im geraden europäischen Schwert (I) und im asiatischen Krummschwert (II). Ein Schwert der Form III lässt sich nicht in eine Scheide stecken. Gibt es weitere Kurven, die eine gleichmäßige Krümmung besitzen?
Haben Sie an die dritte Dimension gedacht? Im Zweidimensionalen sind die Gerade und der Kreisbogen in der Tat die einzigen Kurven mit einer gleichmäßigen Krümmung, aber nimmt man noch die dritte Dimension hinzu, so gibt es noch eine weitere: die Helix. Sie ist besser bekannt unter dem Namen Schraubenlinie, und das deutet schon auf ihre Hauptanwendung in der Technik hin: Keine Schraube ließe sich in eine Mutter drehen, wenn ihr Gewinde nicht eine gleichmäßige Krümmung hätte.



Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.