Hemmes mathematische Rätsel: Sechsecke
Der »National Council of Teachers of Mathematics«, ein Verband amerikanischer Mathematiklehrer, gibt seit über hundert Jahren monatlich die Zeitschrift »The Mathematics Teacher« heraus. Das mittlere Doppelblatt jedes Heftes lässt sich herausnehmen und ist ein Kalender des jeweiligen Monats, der für jeden Tag eine mathematische Denksportaufgabe enthält. Die Aufgaben werden von Lehrern und Schülern zusammengestellt. Ein paar Hundert dieser Kalenderprobleme sind inzwischen zu zwei Büchern zusammengestellt worden. Das erste Buch heißt »Mathematical Challenges for the Middle Grades« und das zweite »Calendar Problems from the Mathematics Teacher«. Das heutige Rätsel ist vom 3. Mai 1999 von Jack G. Roof aus Paulsbo verfasst worden.
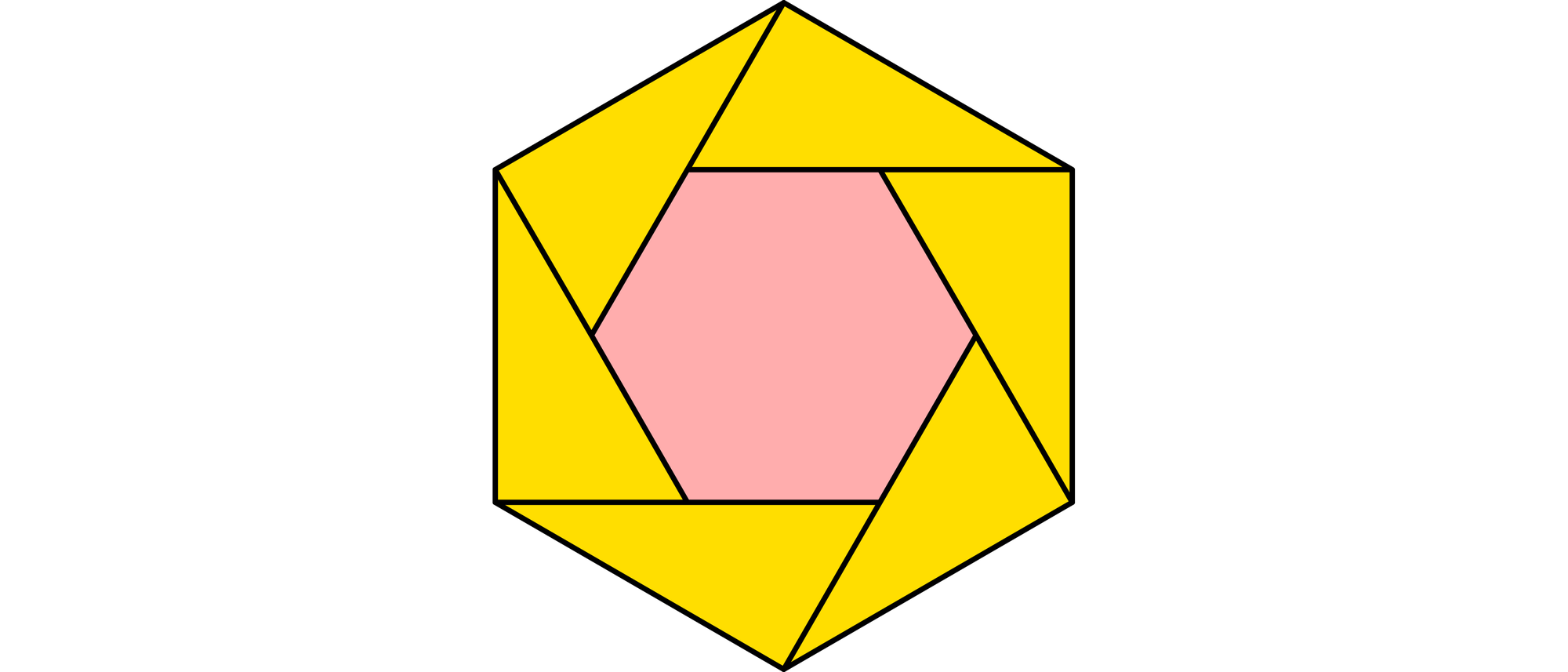
Die Seiten eines regelmäßigen Sechsecks werden, so wie es die Zeichnung zeigt, zu einer Seite hin bis zu ihrer doppelten Länge ausgedehnt. Verbindet man die Endpunkte dieser Strecken, entsteht ein zweites Sechseck, das das ursprüngliche Sechseck umschließt. Das kleine Sechseck hat einen Flächeninhalt von 1 m2. Wie groß ist der Flächeninhalt des großen Sechsecks?
Zeichnet man die Figur in ein Raster aus gleichseitigen Dreiecken ein, so sieht man, dass das innere Sechseck aus sechs Dreiecken und das äußere aus zwölf ganzen und zwölf halben Dreiecken, also insgesamt aus 18 Dreiecken besteht. Das äußere Dreieck ist also dreimal so groß wie das innere und hat somit einen Flächeninhalt von 3 m2.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.