Sehnenviereck
© Spektrum der Wissenschaft / Manon Bischoff (Ausschnitt)
Im ebenen konvexen Sehnenviereck ergänzen sich die gegenüberliegenden Winkel jeweils zu 180°. Wie ist das einfach einzusehen?
Mit diesem Bild:
© Norbert Treitz (Ausschnitt)
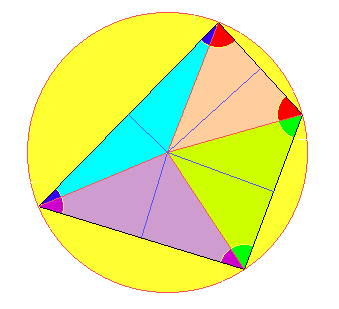
Man verbindet den Kreismittelpunkt mit allen vier Ecken und zerlegt damit das Sehnenviereck in vier gleichschenklige Dreiecke. Die Winkelsumme eines Vierecks beträgt 360°; das ist auch die Summe der Basiswinkel der vier Dreiecke, deren jeder doppelt vorkommt: \(2 \cdot \text{rot} +2 \cdot \text{grün} + 2 \cdot \text{blau} + 2 \cdot \text{lila} = 360°\). Division durch 2 ergibt \( \text{rot} + \text{grün} + \text{blau} + \text{lila} = 180°\). Und in zwei gegenüberliegenden Viereckswinkeln kommt jeder Dreiecks-Basiswinkel genau einmal vor. Also ist deren Summe 180°.



Schreiben Sie uns!
Beitrag schreiben